18．(本题满分16分)

有一座大桥既是交通拥挤地段，又是事故多发地段，为了保证安全，交通部门规定。大桥上的车距d(m)与车速v(km/h)和车长l(m)的关系满足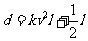：(k为正的常数)，假定车身长为4m，当车速为60(km/h)时，车距为2.66个车身长。

(1)写出车距d关于车速v的函数关系式;

(2)应规定怎样的车速，才能使大桥上每小时通过的车辆最多？

17．(本题满分14分)

　已知圆O的方程为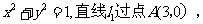且与圆O相切。

(1)求直线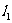的方程；

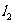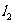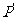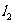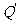(2)设圆O与x轴交与P，Q两点，M是圆O上异于P,Q的任意一点，过点A且与x轴垂直的直线为，直线PM交直线于点，直线QM交直线于点。求证：以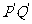为直径的圆C总过定点，并求出定点坐标。

16．(本题满分14分)

在四棱锥O－ABCD中，底面ABCD为菱形，OA⊥平面ABCD，E为OA的中点，F为BC的中点，求证：

(1)平面BDO⊥平面ACO；

(2)EF//平面OCD.

15．(本题满分14分)

在斜三角形ABC中，角A,B,C所对的边分别为a，b，c且.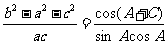

(1)求角A；

(2)若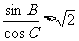，求角C的取值范围。

14．将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则表上数字标签：原点处标0，点(1，0)处标1，点(1，-1)处标2，点(0，-1)处标3，点(-1，-1)处标4，点(-1，0)标5，点(-1，1)处标6，点(0，1)处标7，以此类推，则标签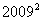的格点的坐标为　 　　　　　　　　

13．函数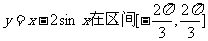上的最大值为　　　　

12．已知平面向量的夹角为，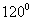　　　　　　

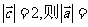
11．已知抛物线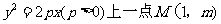到其焦点的距离为5，双曲线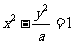的左顶点为A，若双曲线一条渐近线与直线AM垂直，则实数a=　　

10．已知平面区域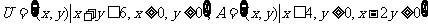，若向区域U内随机投一点P，则点P落入区域A的概率为　　　

9．已知函数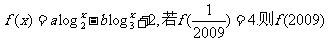的值为