
2.若复数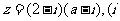 为虚数单位)为纯虚数,则实数a的值为
为虚数单位)为纯虚数,则实数a的值为
1.已知集合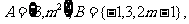 若
若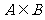 ,则实数m的值为
,则实数m的值为
22.(本小题满分14分)
如图,曲线 的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为
的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为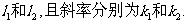
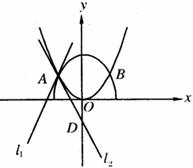
(I) 无关?若是,给出证明;若否,给以说明;
无关?若是,给出证明;若否,给以说明;
(II)若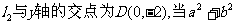 取得最小值9时,求曲线C1与抛物线C2的方程。
取得最小值9时,求曲线C1与抛物线C2的方程。
21.(本小题满分12分)
已知函数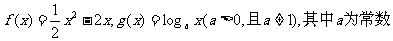 ,如果
,如果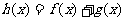 在其定义域上是增函数,且
在其定义域上是增函数,且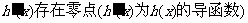 。
。
(I)求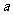 的值;
的值;
(II)设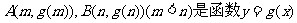 的图象上两点,
的图象上两点,
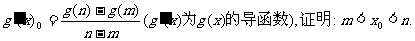
20.(本小题满分12分)
已知数列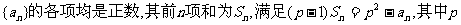 为正常数,且
为正常数,且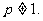
(I)求数列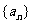 的通项公式;
的通项公式;
(II)设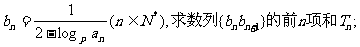
(III)是否存在正整数M,使得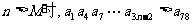 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
19.(本小题满分12分)
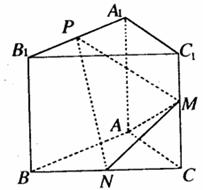
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,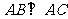 ,M是CC1的中点,N是BC的中点,点P在A1B1上,且满足
,M是CC1的中点,N是BC的中点,点P在A1B1上,且满足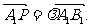
|
(II)当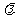 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角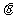 最大?并求该角最大值的正切值;
最大?并求该角最大值的正切值;
(II)若平面PMN与平面ABC所成的二面角为45°,试确定点P的位置。
18.(本小题满分12分)
某车间在两天内,每天生产10件某产品,其中第一天、第二天分别生产了1件、2件次品,而质检部每天要在生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过。
(I)求两天全部通过检查的概率;
(II)若厂内对该车间生产的产品质量采用奖惩制度,两天全不通过检查罚300元,通过1天,2天分别奖300元、900元。那么该车间在这两天内得到奖金的数学期望是多少元?
17.(本小题满分12分)
在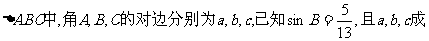 等比数列。
等比数列。
(1)求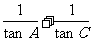 的值;
的值;
(2)若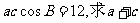 的值。
的值。
16.有以下四个命题:
①若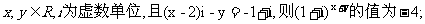
②将函数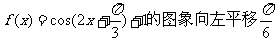 个单位后,对应的函数是偶函数;
个单位后,对应的函数是偶函数;
③若直线 没有交点,则过点(a,b)的直线与椭圆
没有交点,则过点(a,b)的直线与椭圆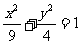 有两个交点;
有两个交点;
④在做回归分析时,残差图中残差点分布的带状区域的宽度越窄相关指数越小。其中所有正确命题的序号为 。
15.定义运算法则如下:
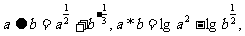
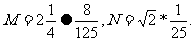
若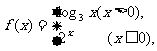 则
则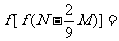 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com