
23. 已知:
已知:
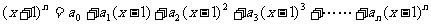
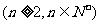

(1)当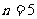 时,求
时,求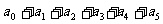 的值.
的值.
(2)设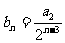 ,
,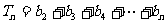 。试用数学归纳法证明: 当
。试用数学归纳法证明: 当 时,
时,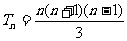

22.已知圆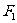 :
: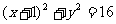 ,定点F2(1,0),动圆M过点
,定点F2(1,0),动圆M过点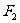 ,且与圆
,且与圆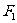 相内切。
相内切。
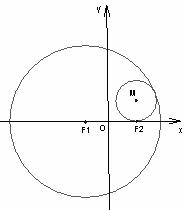
(1)求点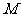 的轨迹
的轨迹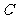 的方程;
的方程;
(2)若过原点的直线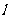 与(1)中的曲线
与(1)中的曲线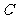 交于
交于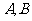 两点,且
两点,且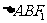 的面积为
的面积为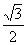 ,
, 学科求直线
学科求直线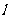 的方程.
的方程.
21.选做题(在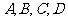 四小题中只能选做2题,每小题10分,共计20分)
四小题中只能选做2题,每小题10分,共计20分)
A.选修 :几何证明选讲
:几何证明选讲
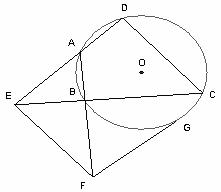
如图,已知四边形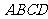 内接于⊙O,
内接于⊙O,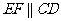 ,
,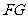 切⊙O于点
切⊙O于点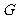 .
.
求证: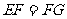 .
.

 B.选修4-2:矩阵与变换
B.选修4-2:矩阵与变换
已知矩阵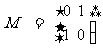 ,
,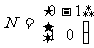 。在平面直角坐标系中,设直线
。在平面直角坐标系中,设直线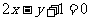 在矩阵
在矩阵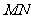 对应的变换作用下得到的曲线
对应的变换作用下得到的曲线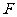 ,求曲线
,求曲线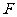 的方程.
的方程. 学
学
C.选修4-4;坐标系与参数方程
已知直线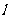 和参数方程为
和参数方程为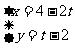
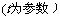 ,
,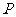 是椭圆
是椭圆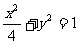 上任意一点,求点
上任意一点,求点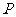 到直线
到直线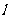 的距离的最大值.
的距离的最大值. 学
学
D.选修4-5:不等式选讲
已知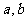 为正数,求证:
为正数,求证: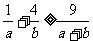 .
.
[必做题]:第22题、第23题每题10分,共20分.
20.(本题满分16分)
在数列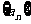 中,已知
中,已知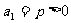 ,且
,且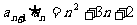 ,
,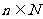
(1)若数列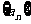 为等差数列,求
为等差数列,求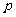 的值.
的值.
(2)求数列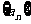 的前
的前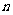 项和
项和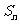 .
.
(3)当 时,求证:
时,求证: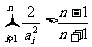 .
.
数学附加题
19.(本题满分16分)
设 ,函数
,函数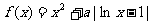 .
.
(1)当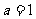 时,求曲线
时,求曲线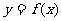 在
在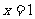 处的切线方程;
处的切线方程;
(2)当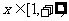 时,求函数
时,求函数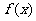 的最小值.
的最小值.
18.(本题满分16分)
在平面直角坐标系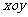 中,已知抛物线
中,已知抛物线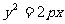 横坐标为4的点到该抛物线的焦点的距离为5.
横坐标为4的点到该抛物线的焦点的距离为5.
(1)求抛物线的标准方程;
(2)设点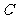 是抛物线上的动点,若以
是抛物线上的动点,若以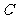 为圆心的圆在
为圆心的圆在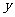 轴上截得的弦长为
轴上截得的弦长为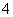 ,求证:
,求证: 圆
圆 过定点.
过定点.
17.(本题满分14分)
已知函数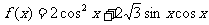 .
.
(1)求函数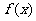 在
在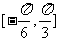 上的值域;
上的值域;
(2)在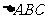 中,若
中,若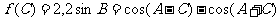 ,求
,求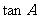 的值.
的值.
16.(本题满分14分)
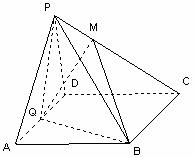
如图,在四棱锥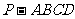 中,底面
中,底面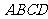 为菱形,
为菱形,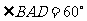 ,
,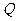 为
为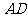 的中点.
的中点. 学
学
(1)若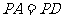 ,求证:平面
,求证:平面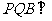 平面
平面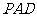 ;
;
(2)点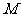 在线段
在线段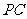 上,
上,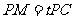 ,试确定实数
,试确定实数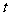 的值,使得
的值,使得 .
.
15.(本题满分14分)
某学校篮球队,羽毛球队、乒乓球队员,某些队员不止参加了一支球队,具体情况如图所示各有10名,现从中随机抽取一名队员,
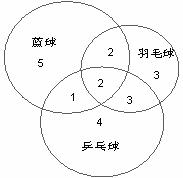
求:(1)该队员只属于一支球队的概率;
 (2)该队员最多属于两支球队的概率
(2)该队员最多属于两支球队的概率
14.已知函数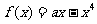 ,
,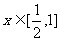 ,
,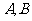 是其图象上不同的两点.若直线
是其图象上不同的两点.若直线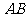 的斜率
的斜率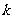 总满足
总满足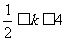 ,则实数
,则实数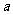 的值是
.
的值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com