
1.如果直线 等于 ( )
等于 ( )
A.-3 B.-6 C.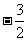 D.
D.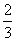
22.(本小题满分14分)
已知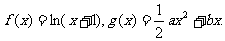
(Ⅰ)若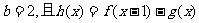 存在单调递减区间,求
存在单调递减区间,求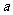 的取值范围;
的取值范围;
(Ⅱ)若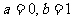 时,求证
时,求证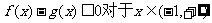 成立;
成立;
(Ⅲ)利用(Ⅱ)的结论证明:若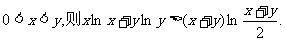
21.(本小题满分12分)
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东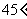 且与点A相距
且与点A相距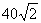 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东 (其中
(其中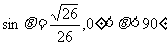 )且与点A相距
)且与点A相距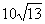 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
20.(本小题满分12分)
已知二次函数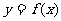 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为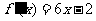 ,数列
,数列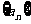 的前n项和为
的前n项和为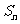 ,点
,点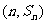 (
(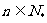 )均在函数
)均在函数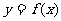 的图像上。
的图像上。
(Ⅰ)求数列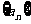 的通项公式;
的通项公式;
(Ⅱ)设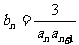 ,
,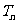 是数列
是数列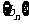 的前n项和,求使得
的前n项和,求使得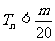 对所有
对所有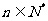 都成立的最小正整数m.
都成立的最小正整数m.
19.(本小题满分12分)
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90° .
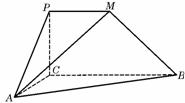
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的余弦值;
(Ⅲ)求多面体P-MABC的体积.
18.(本小题满分12分)
已知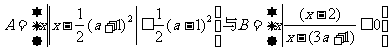 ,其中
,其中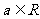 .
.
(Ⅰ)当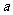 =3时,求
=3时,求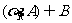 ;
;
(Ⅱ)若命题p: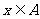 ,q:
,q: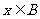 ,且p是q的充分不必要条件,求实数
,且p是q的充分不必要条件,求实数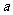 的取值范围.
的取值范围.
17.(本小题满分12分)
设函数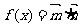 ,其中向量
,其中向量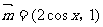 ,
,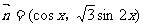 ,
,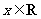 .
.
(Ⅰ)求函数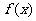 的最小正周期与单调减区间;
的最小正周期与单调减区间;
(Ⅱ)要得到函数y=sinx的图象,需将函数y=f(x)的图象作怎样的变换?
16.给出下列命题:
①函数f(x)=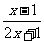 对称中心是(
对称中心是(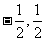 );
);
②已知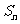 是等差数列{an}(
是等差数列{an}(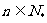 )的前n项和,若
)的前n项和,若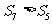 ,则
,则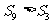 ;
;
③函数f(x)=x|x|+px+q(x∈R)为奇函数的充要条件是q=0;
④已知a,b,m均是正数,且a>b,则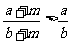
其中真命题的序号是_______.(将所有真命题的序号都填上)
15.已知函数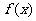 满足
满足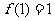 ,且对任何正实数
,且对任何正实数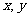 ,均有
,均有
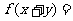
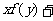
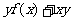 ,则
,则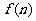 =
(
=
(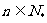 ).
).
14.已知向量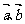 的夹角为120°,且
的夹角为120°,且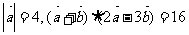 ,则
,则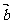 在
在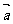 方向上的正射影的数量是 .
方向上的正射影的数量是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com