
3.已知向量a=(-2,2),b=(5,k).若|a+b|不超过5,则k的取值范围是 ( )
A.[-4,6] B.[-6,4] C.[-6,2] D.[-2,6]
2.对任意实数a,b,c,给出下列命题:其中真命题的个数是( )
①“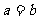 ”是“
”是“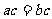 ”充要条件; ②“
”充要条件; ②“ 是无理数”是“a是无理数”的充要条件
是无理数”是“a是无理数”的充要条件
③“a>b”是“a2>b2”的充分条件; ④“a<5”是“a<3”的必要条件.
A.1 B.2 C.3 D.4
1.设P、Q为两个非空实数集合,定义集合P+Q=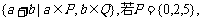
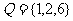 ,则P+Q中元素的个数是( )
,则P+Q中元素的个数是( )
A.9 B.8 C.7 D.6
(15)(本小题共12分)
已知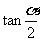 =2,求:
=2,求:
(Ⅰ)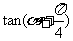 的值;
的值;
(Ⅱ)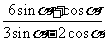 的值.
的值.
(16)(本小题共14分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
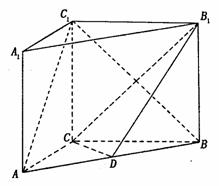
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC 1//平面CDB1;
(Ⅲ)求异面直线AC1与B1C所成角的余弦值.
(17)(本小题共13分)
数列{an}的前n项和为Sn,且a1=1,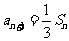 ,n=1,2,3,……,求:
,n=1,2,3,……,求:
(Ⅰ)a2,a3,a4的值及数列{an}的通项公式;
(Ⅱ)a2+ a4+ a6+…+ a2n的值.
(18)(本小题共13分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为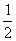 ,乙每次击中目标的概率
,乙每次击中目标的概率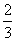 .求:
.求:
(Ⅰ)甲恰好击中目标2次的概率;
(Ⅱ)乙至少击中目标2次的概率;
(Ⅲ)求乙恰好比甲多击中目标2次的概率.
(19)(本小题共14分)
已知函数f(x)=-x3+3x2+9x+a.
(Ⅰ)求f(x)的单调递减区间;
(Ⅱ)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
(20)(本小题共14分)
如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
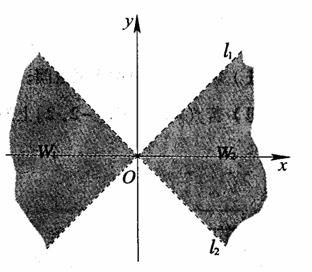
(Ⅰ)分别用不等式组表示W1和W2;
(Ⅱ)若区域W中的动点P(x,y)到l1,l2的距离之积等于d2,求点P的轨迹C的方程;
(Ⅲ)设不过原点O的直线l与(Ⅱ)中的曲线C相交于M1,M2两点,且与l1,l2分别交于M3,M4两点.求证△OM1M2的重心与△OM3M4的重心重合.
(9)抛物线y2=4x的准线方程是 ,焦点坐标是 .
(10)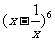 的展开式中的常数项是
(用数字作答)
的展开式中的常数项是
(用数字作答)
(11)函数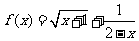 的定义域为
.
的定义域为
.
(12)在△ABC中,AC=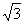 ,∠A=45°,∠C=75°,则BC的长为
.
,∠A=45°,∠C=75°,则BC的长为
.
(13)对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)·f(x2); ②f(x1·x2)=f(x1)+f(x2);
③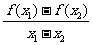 >0;
④
>0;
④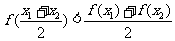 .
.
当f(x)=lg x时,上述结论中正确结论的序号是 .
(14)已知n次多项式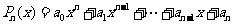 .
.
如果在一种算法中,计算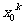 (k=2,3,4,…,n)的值需要k-1次乘法,计算
(k=2,3,4,…,n)的值需要k-1次乘法,计算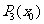 的值共需要9次运算(6次乘法,3次加法),那么计算
的值共需要9次运算(6次乘法,3次加法),那么计算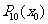 的值共需要
次运算.
的值共需要
次运算.
下面给出一种减少运算次数的算法: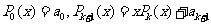 (k=0,1,2,…,n-1).利用该算法,计算
(k=0,1,2,…,n-1).利用该算法,计算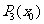 的值共需要6次运算,计算
的值共需要6次运算,计算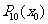 的值共需要
次运算.
的值共需要
次运算.
(1)设集合M={x| x>1},P={x| x2>1},则下列关系中正确的是
(A)M=P (B)P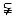 M (C)M
M (C)M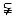 P ( D)M∪P=R
P ( D)M∪P=R
(2)为了得到函数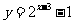 的图象,只需把函数
的图象,只需把函数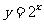 的图象上所有点
的图象上所有点
(A)向右平移3个单位长度,再向下平移1个单位长度
(B)向左平移3个单位长度,再向下平移1个单位长度
(C)向右平移3个单位长度,再向上平移1个单位长度
(D)向左平移3个单位长度,再向上平移1个单位长度
(3)“m=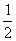 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
(A)充分必要条件 (B)充分而不必要条件
(C)必要而不充分条件 (D)既不充分也不必要条件
(4)若|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为
(A)30° (B)60° (C)120° (D)150°
(5)从原点向圆 x2+y2-12y+27=0作两条切线,则这两条切线的夹角的大小为
(A)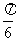 (B)
(B)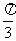 (C)
(C)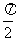 (D)
(D)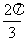
(6)对任意的锐角α,β,下列不等关系中正确的是
(A)sin(α+β)>sinα+sinβ (B)sin(α+β)>cosα+cosβ
(C)cos(α+β)<sinα+sinβ (D)cos(α+β)<cosα+cosβ
(7)在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是
(A)BC//平面PDF (B)DF⊥平面PAE
(C)平面PDF⊥平面ABC (D)平面PAE⊥平面ABC
(8)五个工程队承建某项工程的5个不同的子项目,每个工程队承建1项,其中甲工程队不能承建1号子项目,则不同的承建方案共有
(A)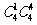 种
(B)
种
(B)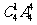 种 (C)
种 (C)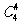 种 (D)
种 (D)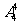 种
种
第Ⅱ卷(共110分)
21、(本小题满分14分)
已知函数f(x)=lnx,g(x)=-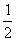 ax2+bx,a≠0。
ax2+bx,a≠0。
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行。
20、(本小题满分14分)
自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响。用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0。不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正常数a,b,c。
(Ⅰ)求xn+1与xn的关系式;
(Ⅱ)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
(Ⅲ)设a=2,c=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的最大允许值是多少?证明你的结论。
19、(本小题满分14分)
已知椭圆C: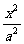 +
+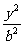 =1(a>b>0)的左、右焦点为F1、F2,离心率为e。直线l:y=ex+a与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左、右焦点为F1、F2,离心率为e。直线l:y=ex+a与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设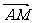 =λ
=λ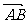 。
。
(Ⅰ)证明:λ=1-e2
(Ⅱ)确定λ的值,使得△PF1F2是等腰三角形。
18、(本小题满分14分)
某城市有甲、乙、丙3个旅游景点,一位客人游览这3个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没游览的景点数之差的绝对值。
(Ⅰ)求ξ的分布列及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞)上单调递增”为事件A,求事件A的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com