
(17)(本小题满分12分)
已知函数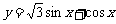 ,
,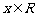 。
。
(I)当函数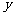 取得最大值时,求自变量
取得最大值时,求自变量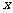 的集合;
的集合;
(II)该函数的图象可由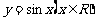 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(18)(本小题满分12分)
设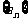 为等差数列,
为等差数列,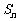 为数列
为数列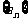 的前
的前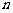 项和,已知
项和,已知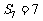 ,
,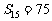 ,
,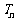 为数列
为数列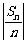 的前
的前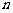 项和,求
项和,求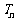 。
。
(19)(本小题满分12分)
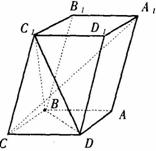
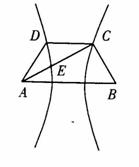
如图,已知平行六面体ABCD-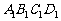 的底面ABCD是菱形,且
的底面ABCD是菱形,且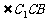
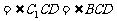 。
。
(I)证明: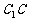 ⊥BD;
⊥BD;
(II)当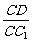 的值为多少时,能使
的值为多少时,能使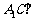 平面
平面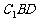 ?请给出证明。
?请给出证明。
(20)(本小题满分12分)
设函数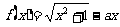 ,其中
,其中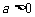 。
。
(I)解不等式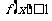 ;
;
(II)证明:当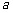
 时,函数
时,函数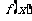 在区间
在区间 上是单调函数。
上是单调函数。
(21)(本小题满分12分)
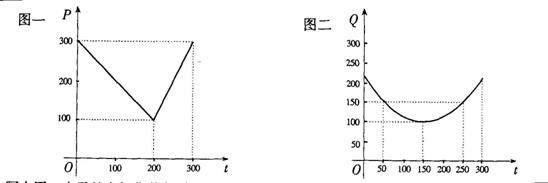
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
I)
写出图一表示的市场售价与时间的函数关系式P= ;
;
写出图二表示的种植成本与时间的函数关系式Q=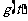 ;
;
I 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/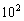 kg,时间单位:天)
kg,时间单位:天)
(22)(本小题满分14分)
如图,已知梯形ABCD中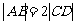 ,点E分有向线段
,点E分有向线段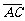 所成的比为
所成的比为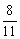 ,双曲线过C、D、E三点,且以A、B为焦点。求双曲线的离心率。
,双曲线过C、D、E三点,且以A、B为焦点。求双曲线的离心率。
(13)乒乓球队的10名队员中有3名主力队员,派5名参加比赛。3名主力队员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四位置,那么不同的出场安排共有_____种(用数字作答)。
(14)椭圆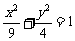 的焦点为
的焦点为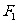 、
、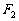 ,点P为其上的动点,当
,点P为其上的动点,当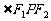 为钝角时,点P横坐标的取值范围是________。
为钝角时,点P横坐标的取值范围是________。
(15)设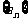 是首项为1的正项数列,且
是首项为1的正项数列,且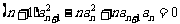 (
(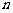 =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是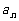 =________。
=________。
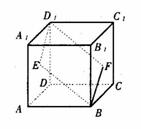
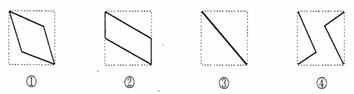
(16)如图,E、F分别为正方体的面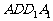 、面
、面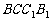 的中心,则四边形
的中心,则四边形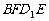 在该正方体的面上的射影可能是_______。(要求:把可能的图的 序号都填上)
在该正方体的面上的射影可能是_______。(要求:把可能的图的 序号都填上)
(1)设集合A=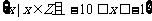 ,B=
,B=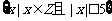 ,则A∪B中的元素个数是
,则A∪B中的元素个数是
(A)11 (B)10 (C)16 (D)15
(2)在复平面内,把复数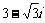 对应的向量按顺时针方向旋转
对应的向量按顺时针方向旋转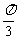 ,所得向量对应的复数是
,所得向量对应的复数是
(A)2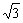 (B)
(B)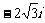 (C)
(C)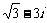 (D)3
(D)3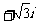
(3)一个长方体共一项点的三个面的面积分别是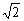 ,
,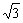 ,
,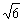 ,这个长方体对角线的长是
,这个长方体对角线的长是
(A)2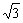 (B)3
(B)3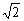 (C)6 (D)
(C)6 (D)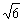
(4)已知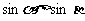 ,那么下列命题成立的是
,那么下列命题成立的是
(A)若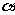 、
、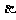 是第一象限角,则
是第一象限角,则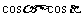
(B)若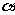 、
、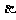 是第二象限角,则
是第二象限角,则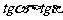
(C)若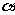 、
、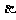 是第三象限角,则
是第三象限角,则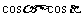
(D)若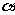 、
、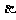 是第四象限角,则
是第四象限角,则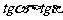
(5)函数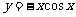 的部分图象是
的部分图象是

(6)《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过
800元的部分不必纳税,超过800元的部分为全月应纳税所得额。此项税
款按下表分段累进计算:
|
全月应纳税所得额 |
税率 |
|
不超过500元的部分 |
5% |
|
超过500元至2000元的部分 |
10% |
|
超过2000元至5000元的部分 |
15% |
|
… |
… |
某人一月份应交纳此项税款26.78元,则他的当月工资、薪金所得介于
(A)800~900元 (B)900~1200元 (C)1200~1500元 (D)1500~2800元
(7)若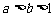 ,P=
,P=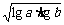 ,Q=
,Q=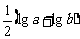 ,R=
,R=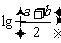 ,则
,则
(A)R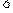 P
P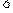 Q (B)P
Q (B)P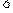 Q
Q 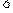 R (C)Q
R (C)Q 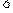 P
P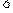 R
(D)P
R
(D)P 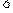 R
R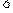 Q
Q
(8)已知两条直线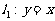 ,
,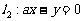 ,其中
,其中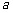 为实数。当这两条直线的夹角在
为实数。当这两条直线的夹角在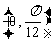 内变动时,
内变动时,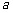 的取值范围是
的取值范围是
(A)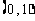 (B)
(B)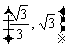 (C)
(C)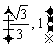 ∪
∪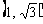 (D)
(D)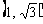
(9)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是
(A)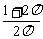 (B)
(B)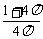 (C)
(C)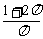 (D)
(D)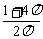
(10)过原点的直线与圆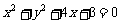 相切,若切点在第三象限,则该直线的方程是
相切,若切点在第三象限,则该直线的方程是
(A)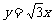 (B)
(B)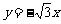 (C)
(C)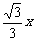 (D)
(D)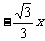
(11)过抛物线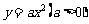 的焦点F作一条直线交抛物线于P、Q两点,若线段PF与FQ的长分别是
的焦点F作一条直线交抛物线于P、Q两点,若线段PF与FQ的长分别是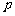 、
、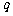 ,则
,则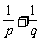 等于
等于
(A)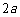 (B)
(B)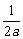 (C)
(C)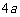 (D)
(D)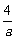
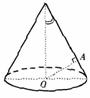
(12)如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为
(A)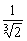 (B)
(B)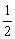 (C)
(C)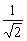 (D)
(D)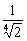
第II卷(非选择题 90分)
(17)(本小题满分12分)
已知函数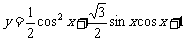 ,
,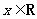 .
.
(I)当函数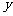 取得最大值时,求自变量
取得最大值时,求自变量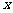 的集合;
的集合;
(II)该函数的图像可由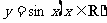 的图像经过怎样的平移和伸缩变换得到?
的图像经过怎样的平移和伸缩变换得到?
(18)(本小题满分12分)
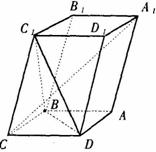
如图,已知平行六面体ABCD-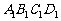 的底面ABCD是菱形,且
的底面ABCD是菱形,且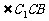 =
=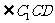 =
=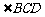 =
=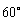 .
.
(I)证明: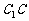 ⊥BD;
⊥BD;
(II)假定CD=2,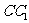 =
=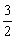 ,记面
,记面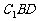 为
为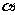 ,面CBD为
,面CBD为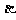 ,求二面角
,求二面角 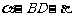 的平面角的余弦值;
的平面角的余弦值;
(III)当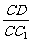 的值为多少时,能使
的值为多少时,能使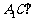 平面
平面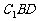 ?请给出证明.
?请给出证明.
(19)(本小题满分12分)
设函数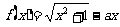 ,其中
,其中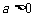 .
.
(I)解不等式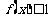 ;
;
(II)求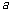 的取值范围,使函数
的取值范围,使函数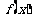 在区间
在区间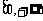 上是单调函数.
上是单调函数.
(20)(本小题满分12分)
(I)已知数列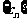 ,其中
,其中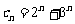 ,且数列
,且数列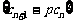 为等比数列,求常数
为等比数列,求常数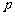 ;
;
(II)设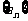 、
、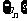 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,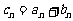 ,证明数列
,证明数列 不是等比数列.
不是等比数列.
(21)(本小题满分12分)
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
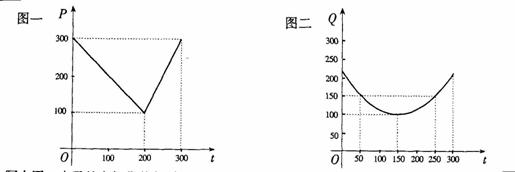
(Ⅰ)写出图一表示的市场售价与时间的函数关系式P= ;
;
写出图二表示的种植成本与时间的函数关系式Q=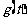 ;
;
(Ⅱ)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/ kg,时间单位:天)
kg,时间单位:天)
(22)(本小题满分14分)
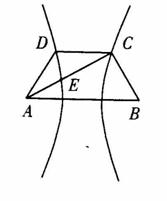
如图,已知梯形ABCD中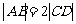 ,点E分有向线段
,点E分有向线段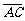 所成的比为
所成的比为 ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当 时,求双曲线离心率
时,求双曲线离心率 的取值范围.
的取值范围.
(13)乒乓球队的10名队员中有3名主力队员,派5名参加比赛.3名主力队员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四位置,那么不同的出场安排共有_____种(用数字作答).
(14)椭圆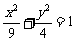 的焦点为
的焦点为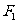 、
、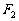 ,点P为其上的动点,当
,点P为其上的动点,当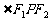 为钝角时,点P 横坐标的取值范围是________.
为钝角时,点P 横坐标的取值范围是________.
(15)设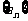 是首项为1的正项数列,且
是首项为1的正项数列,且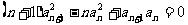 (
(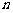 =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是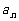 =________.
=________.
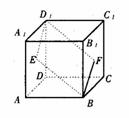
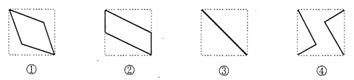
(16)如图,E、F分别为正方体的面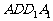 、面
、面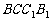 的中心,则四边形
的中心,则四边形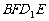 在该正方体的面上的射影可能 是_______.(要求:把可能的图的序号都填上)
在该正方体的面上的射影可能 是_______.(要求:把可能的图的序号都填上)
(1)设集合A和B都是自然数集合N,映射 把集合A中的元素
把集合A中的元素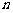 映射到集合B 中的元素
映射到集合B 中的元素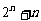 ,则在映射
,则在映射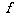 下,象20的原象是
下,象20的原象是
(A) 2 (B) 3 (C) 4 (D) 5
(2)在复平面内,把复数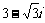 对应的向量按顺时针方向旋转
对应的向量按顺时针方向旋转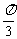 ,所得向量对应的复数是
,所得向量对应的复数是
(A) 2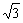 (B)
(B) 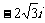 (C)
(C) 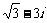 (D) 3
(D) 3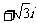
(3)一个长方体共一顶点的三个面的面积分别是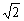 ,
,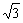 ,
,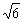 ,这个长方体对角线的长是
,这个长方体对角线的长是
(A) 2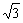 (B) 3
(B) 3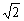 (C) 6 (D)
(C) 6 (D) 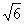
(4)已知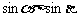 ,那么下列命题成立的是
,那么下列命题成立的是
(A)若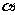 、
、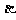 是第一象限角,则
是第一象限角,则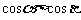
(B)若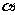 、
、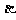 是第二象限角,则
是第二象限角,则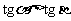
(C)若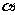 、
、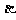 是第三象限角,则
是第三象限角,则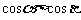
(D)若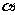 、
、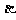 是第四象限角,则
是第四象限角,则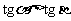
(5)函数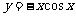 的部分图像是
的部分图像是

(6)《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的部分不必纳税,超过800元的部分为全月应纳税所得额.此项税款按下表分段累进计算:
|
全月应纳税所得额 |
税率 |
|
不超过500元的部分 |
5% |
|
超过500元至2000元的部分 |
10% |
|
超过2000元至5000元的部分 |
15% |
|
… |
… |
某人一月份应交纳此项税款26.78元,则他的当月工资、薪金所得介于
(A) 800~900元 (B) 900~1200元
(C) 1200~1500元 (D) 1500~2800元
(7)若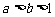 ,P=
,P=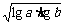 ,Q=
,Q=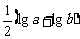 ,R=
,R=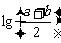 ,则
,则
(A) R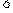 P
P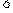 Q (B) P
Q (B) P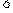 Q
Q 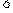 R
R
(C) Q 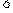 P
P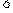 R (D) P
R (D) P 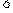 R
R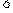 Q
Q
(8)以极坐标系中的点 为圆心,1为半径的圆的方程是
为圆心,1为半径的圆的方程是
(A) 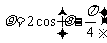 (B)
(B) 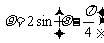
(C) 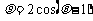 (D)
(D) 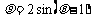
(9)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是
(A) 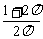 (B)
(B) 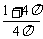 (C)
(C) 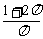 (D)
(D) 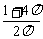
(10)过原点的直线与圆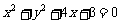 相切,若切点在第三象限,则该直线的方程是
相切,若切点在第三象限,则该直线的方程是
(A) 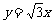 (B)
(B) 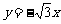 (C)
(C) 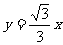 (D)
(D) 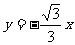
(11)过抛物线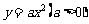 的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是
的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是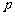 、
、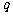 ,则
,则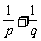 等于
等于
(A) 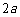 (B)
(B) 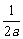 (C)
(C) 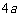 (D)
(D) 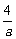
(12)如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角为
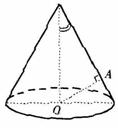 (A)
(A)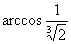 (B)
(B)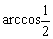 (C)
(C)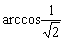 (D)
(D)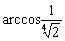
第II卷(非选择题共90分)
(17)
已知等差数列前三项为a,4,3a,前n项和为Sn,Sk = 2550.
(Ⅰ)求a及k的值;
(Ⅱ)求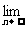 (
(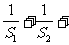 …
…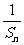 ).
).
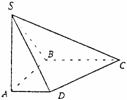
(18)
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC = 90°,SA⊥面ABCD,SA = AB = BC
= 1,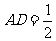 .
.
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
(19) 已知圆内接四边形ABCD的边长分别为AB = 2,BC = 6,CD = DA = 4 求四边形ABCD的面积.
(20) 设抛物线y2 =2px (p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴.证明直线AC经过原点O.
(21) 设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ (λ<1=,画面的上、下各留8cm空白,左、右各留5cm空白.怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?
(22)(本小题满分14分)
设f (x) 是定义在R上的偶函数,其图像关于直线x = 1对称.对任意x1,x2∈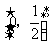 都有f (x1+x2) = f (x1) · f (x2).
都有f (x1+x2) = f (x1) · f (x2).
(Ⅰ)求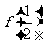 及
及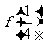 ;
;
(Ⅱ)证明f (x) 是周期函数;
(13) (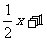 )10的二项展开式中x 3的系数为
.
)10的二项展开式中x 3的系数为
.
(14) 双曲线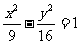 的两个焦点为F1、F2,点P在双曲线上.若PF1⊥PF2,则点P到x轴的距离为
.
的两个焦点为F1、F2,点P在双曲线上.若PF1⊥PF2,则点P到x轴的距离为
.
(15) 设{an}是公比为q的等比数列,Sn是它的前n项和.若{Sn}是等差数列,则q = .
(16) 圆周上有2n个等分点(n>1),以其中三个点为顶点的直角三角形的个数为 ________ .
(1) tg300°+ctg405°的值为
(A) 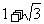 (B)
(B) 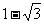 (C)
(C) 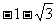 (D)
(D) 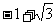
(2)过点A (1,-1)、B (-1,1)且圆心在直线x+y-2 = 0上的圆的方程是
(A) (x-3)2+(y+1)2 = 4 (B) (x+3)2+(y-1)2 = 4
(C) (x-1)2+(y-1)2 = 4 (D) (x+1)2+(y+1)2 = 4
(3) 若一个圆锥的轴截面是等边三角形,其面积为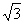 ,则这个圆锥的面积是
,则这个圆锥的面积是
(A) 3π (B) 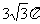 (C) 6π (D) 9π
(C) 6π (D) 9π
(4) 若定义在区间(-1,0)内的函数f (x) = log2a(x+1)满足f (x)>0,则a的取值范围是
(A)(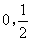 ) (B)
) (B) 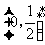 (C) (
(C) (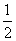 ,+∞) (D) (0,+∞)
,+∞) (D) (0,+∞)
(5) 已知复数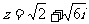 ,则
,则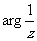 是
是
(A) 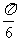 (B)
(B) 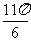 (C)
(C) 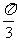 (D)
(D) 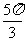
(6)函数y = 2-x+1(x>0)的反函数是
(A)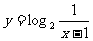 ,x∈(1,2) (B)
,x∈(1,2) (B) 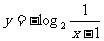 ,x∈(1,2)
,x∈(1,2)
(C) 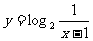 ,
,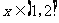 (D)
(D) 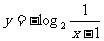 ,
,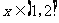
(7) 若椭圆经过原点,且焦点为F1 (1,0) F2 (3,0),则其离心率为
(A) 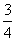 (B)
(B) 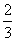 (C)
(C) 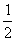 (D)
(D) 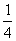
(8)若0<α<β<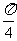 ,sin α+cos α = α,sin β+cos β= b,则
,sin α+cos α = α,sin β+cos β= b,则
(A) a<b (B) a>b (C) ab<1 (D) ab>2
(9)在正三棱柱ABC-A1B1C1中,若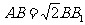 ,则AB1 与C1B所成的角的大小为
,则AB1 与C1B所成的角的大小为
(A) 60° (B) 90° (C) 105° (D) 75°
(10) 设f (x)、g (x)都是单调函数,有如下四个命题:
① 若f (x)单调递增,g (x)单调递增,则f (x)-g (x)单调递增;
② 若f (x)单调递增,g (x)单调递减,则f (x)-g (x)单调递增;
③ 若f (x)单调递减,g (x)单调递增,则f (x)-g (x)单调递减;
④ 若f (x)单调递减,g (x)单调递增,则f (x)-g (x)单调递减.
其中,正确的命题是
(A) ①③ (B) ①④ (C) ②③ (D) ②④
(11)一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P1、P2、P3.
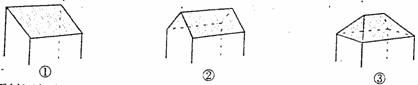
若屋顶斜面与水平面所成的角都是α,则
(A) P3>P2>P1 (B) P3>P2 = P1 (C) P3 = P2>P1 (D) P3 = P2 = P1
(12) 如图,小圆圈表示网络的结点,结点之间的连线表示它 们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为
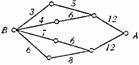
(A) 26 (B) 24 (C) 20 (D) 19
第Ⅱ卷
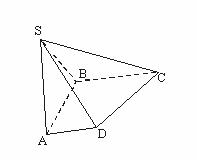
(17)(本小题满分12分)
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=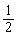 .
.
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
(18)(本小题满分12分)
已知复数z1=i (1-i )3.
(Ⅰ)求arg z1及| z |;
(Ⅱ)当复数z满足| z |=1,求| z-z1 |的最大值.
(19)(本小题满分12分)
设抛物线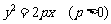 的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴.证明直线AC经过原点O.
的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴.证明直线AC经过原点O.
(20)(本小题满分12分)
已知i,m,n是正整数,且1<i≤m<n.
(Ⅰ)证明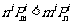 ;
;
(Ⅱ)证明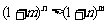 .
.
(21)(本小题满分12分)
从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入800万元,以后每年投入将比上年减少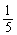 .本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
.本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加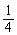 .
.
(Ⅰ)设n年内(本年度为第一年)总投人为an万元,旅游业总收入为bn万元.写出an,bn的表达式;
(Ⅱ)至少经过几年旅游业的总收人才能超过总投入?
(22)(本小题满分12分)
设f (x)是定义在R上的偶函数。其图象关于直线y=x对称,对任意x1,x2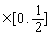 ,都有f (x1+x2)=f (x1)·f (x2),且f ( 1
)=a>0.
,都有f (x1+x2)=f (x1)·f (x2),且f ( 1
)=a>0.
(Ⅰ)求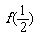 及
及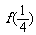 ;
;
(Ⅱ)证明f (x)是周期函数;
(Ⅲ)记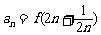 ,求
,求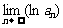 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com