
(13)在下列关于直线l、m与平面α、β的命题中,真命题是
(A)若l β且α⊥β,则l⊥α. (B)若l⊥β且α∥β,则l⊥α.
β且α⊥β,则l⊥α. (B)若l⊥β且α∥β,则l⊥α.
(C)若l⊥β且α⊥β,则l∥α. (D)若α∩β=m且l∥m,则l∥α.
(14)三角方程2sin(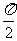 -x)=1的解集为
-x)=1的解集为
(A){x│x=2kπ+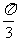 ,k∈Z}. (B){x│x=2kπ+
,k∈Z}. (B){x│x=2kπ+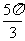 ,k∈Z}.
,k∈Z}.
(C){x│x=2kπ±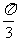 ,k∈Z}. (D){x│x=kπ+(-1)K,k∈Z}.
,k∈Z}. (D){x│x=kπ+(-1)K,k∈Z}.
(15)若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则f(x)=
(A)10x-1. (B)1-10x. (C)1-10-x. (D)10-x-1.
(16)某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
|
行业名称 |
计算机 |
机械 |
营销 |
物流 |
贸易 |
|
应聘人数 |
215830 |
200250 |
154676 |
74570 |
65280 |
|
行业名称 |
计算机 |
营销 |
机械 |
建筑 |
化工 |
|
招聘人数 |
124620 |
102935 |
89115 |
76516 |
70436 |
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是
(A)计算机行业好于化工行业. (B)建筑行业好于物流行业.
(C)机械行业最紧张. (D)营销行业比贸易行业紧张.
(1)若tgα=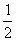 ,则tg(α+
,则tg(α+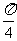 )= .
)= .
(2)设抛物线的顶点坐标为(2,0),准线方程为x=-1,则它的焦点坐标为 .
(3)设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B= .
(4)设等比数列{an}(n∈N)的公比q=-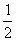 ,且
,且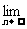 (a1+a3+a5+…+a2n-1)=
(a1+a3+a5+…+a2n-1)=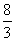 ,则a1= .
,则a1= .
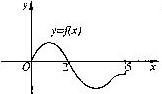
(5)设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时, f(x)的图象如右图,则不等式f(x)<0的解是 .
(6)已知点A(-1,5)和向量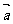 ={2,3},若
={2,3},若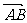 =3
=3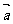 ,则点B的坐标为
.
,则点B的坐标为
.
2≤x≤4
(7)当x、y满足不等式组 y≥3 时,目标函数k=3x-2y的最大值为 . x+y≤8
(8)圆心在直线x=2上的圆C与y轴交于两点A(0, -4),B(0, -2),则圆C的方程为 .
(9)若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是 . (结果用分数表示)
(10)若函数f(x)= a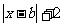 在[0,+∞]上为增函数,则实数a、b的取值范围是
.
在[0,+∞]上为增函数,则实数a、b的取值范围是
.
(11)教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是 .
(12)若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号) ①S1与S2; ②a2与S3; ③a1与an; ④q与an.
其中n为大于1的整数, Sn为{an}的前n项和.
(17)(本小题满分12分)
在等比数列{an}中,已知a6-a4=24,a3·a5=64.求{an}前8项的和S8.
(18)(本小题满分12分)
已知sin22+sin2cos-cos2=1,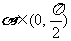 .求sin、tan 的值.
.求sin、tan 的值.
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分.
(19甲)(本小题满分12分)
如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为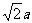 .
.
(Ⅰ)建立适当的坐标系,并写出点A、B、A1、C1的坐标;
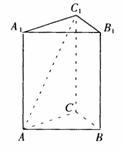
(Ⅱ)求AC1与侧面ABB1A1所成的角.
(19乙)(本小题满分12分)
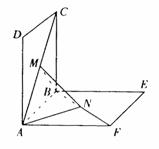
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a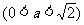 .
.
(Ⅰ)求MN的长;
(Ⅱ)当a为何值时,MN的长最小;
(Ⅲ)当MN长最小时,求面MNA与面MNB所成的二面角 的大小.
(20)(本小题满分12分)
某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5(相互独立).
(Ⅰ)求至少3人同时上网的概率;
(Ⅱ)至少几人同时上网的概率小于0.3?
(21)(本小题满分12分)
已知a>0,函数f(x)=x3-a,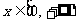 .设x1>0,记曲线y= f(x)在点M(x1,f(x1))处的切线为l.
.设x1>0,记曲线y= f(x)在点M(x1,f(x1))处的切线为l.
(Ⅰ)求l的方程;
(Ⅱ)设l与x轴交点为(x2,0).证明:
(i)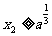 ;
;
(ii)若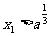 ,则
,则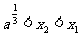 .
.
(22)(本小题满分14分)
已知两点M(-1,0),N(1,0),且点P使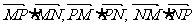 成公差小于零的等差数列.
成公差小于零的等差数列.
(Ⅰ)点P的轨迹是什么曲线?
(Ⅱ)若点P坐标为(x0,y0),为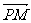 与
与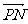 的夹角,求tan.
的夹角,求tan.
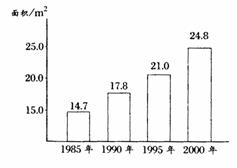
(13)据新华社2002年3月12日电,1985年到2000年间,我国农村人均居住面积如图所示,其中,从________年到________年的五年间增长最快.
(14)已知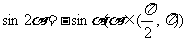 ,则cot =_______________.
,则cot =_______________.
(15)甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位:t/hm2):
|
品种 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
|
甲 |
9.8 |
9.9 |
10.1 |
10 |
10.2 |
|
乙 |
9.4 |
10.3 |
10.8 |
9.7 |
9.8 |
其中产量比较稳定的小麦品种是______________.
(16)设函数f(x)在(-∞,+∞)内有定义,下列函数.
①y=-| f(x)| ②y=xf(x2)
③y=-f(-x) ④y= f(x)-f(-x)
中必为奇函数的有________________.(要求填写正确答案的序号)
(1)若直线(1+a)x+y+1=0与圆x2+y2-2x=0相切,则a的值为
(A)1,-1 (B)2,-2 (C)1 (D)-1
(2)已知m,n为异面直线,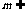 平面 ,
平面 ,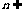 平面 ,
平面 ,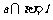 ,则l
,则l
(A)与m,n都相交 (B)与m,n中至少一条相交
(C)与m,n都不相交 (D)至多与m,n中的一条相交
(3)不等式(1+x)(1-|x|)>0的解集是
(A)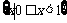 (B)
(B)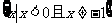
(C)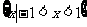 (D)
(D)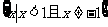
(4)函数y=ax在[0,1]上的最大值与最小值的和为3,则a的值为
(A)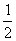 (B)2 (C)4 (D)
(B)2 (C)4 (D)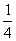
(5)在(0,2)内,使sin x>cos x成立的x取值范围为
(A)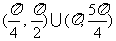 (B)
(B)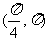
(C)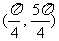 (D)
(D)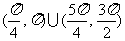
(6)设集合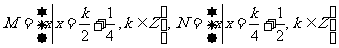 则
则
(A)M=N (B)M N (C)M N (D)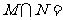 Ø
Ø
(7)椭圆5x2+ky2=5的一个焦点是(0,2),那么k=
(A)-1 (B)1 (C)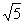 (D)
(D)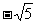
(8)正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为l,侧棱长为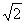 ,则这个棱柱的侧面对角线E1D与BC1所成的角是
,则这个棱柱的侧面对角线E1D与BC1所成的角是
(A)900 (B)600 (C)450 (D)300
(9)函数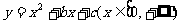 是单调函数的充要条件是
是单调函数的充要条件是
(A)b≥0 (B)b≤0 (C)b>0 (D)b<0
(10)已知0<x<y<a<1,则有
(A)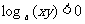 (B)0<log a(xy)<1
(B)0<log a(xy)<1
(C)1<log a(xy)<2 (D)log a(xy)>2
(11)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
(A)8种 (B)12种 (C)16种 (D)20种
(12)平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足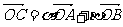 ,其中、∈R,且+=1,则点C的轨迹方程为
,其中、∈R,且+=1,则点C的轨迹方程为
(A)(x-1)2+(y-2)2=5 (B)3x+2y-11=0
(C)2x-y=0 (D)x+2y-5=0
第Ⅱ卷(非选择题共90分)
(17)(本题满分12分)

如图,在直-棱柱ABO-ABO中,OO = 4,OA = 4 , OB = 3 , ∠AOB=90°,D是线段AB的中点,P是侧棱BB上的一点,若OP⊥BD,求OP与底面AOB所成角的大小(结果用反三角函数值表示)
(18)(本题满分12分)
已知点A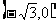 和B
和B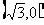 ,动点A、B两点的距离之差的绝对值为2,点C的轨迹与直线y=x-2交于D、E两点,求线段DE的长.
,动点A、B两点的距离之差的绝对值为2,点C的轨迹与直线y=x-2交于D、E两点,求线段DE的长.
(19)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数f(x)=x2 | 2ax+2,x∈[-5,5].
(1)当a =-1时,求函数f(x)的最大值与最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.
(20)(本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分。
某商场在促销期间规定:商场内所有商品按标价的80%出售,同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:

根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为300元,获得的优惠额为:400×0.2+30=110(元),设购买商品得到的优惠率= ,试问:
,试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不小于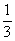 的优惠率?
的优惠率?
(21)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分).
已知函数f(x)=a·bx的图象过点A(4、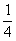 )和B(5,1).
)和B(5,1).
(1)求函数f(x)的解析式;
(2)记an-log2 f (n)、n是正整数,Sn是数列{an}的前n项和,解关于n的不等式anSn≤0;
(3)对于(2)中的an与Sn,整数96是否为数列{anSn}中的项?若是,则求出相应的项数;若不是,则说明理由。
(22)(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分)。
规定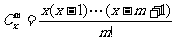 ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且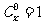 ,这是组合数
,这是组合数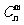 (n、m是正整数,且m≤n)的一种推广。
(n、m是正整数,且m≤n)的一种推广。
(1)求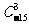 的值;
的值;
(2)设x>0,当x为何值时,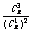 取得最小值?
取得最小值?
(3)组合数的两个性质;
①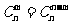 . ②
. ②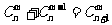 .
.
是否都能推广到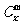 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
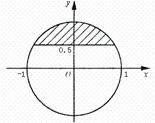
(13)如图,与复平面中的阴影部分(含边界)对应的复数集合是
(A)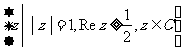 .(B)
.(B)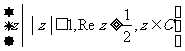 .
.
(C)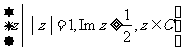 .(D)
.(D)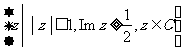 .
.
(14)已知直线l、m,平面 、 ,且l⊥ ,m ,给出下列四个命题;
(1)若 ∥ ,则l⊥m . (2)若则l⊥m , ∥ .
(3)若 ⊥ ,则l∥m . (4)若则l∥m , ⊥ .
其中正确命题的个数是
(A)1个. (B)2个. (C)3个. (D)4个.
(15)函数y=x+sin| x |,x∈[-,]的大致图象是
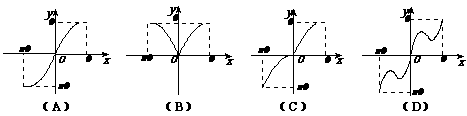
(16)一般地,家庭用电量(千瓦时)与气温(℃)有一定的关系,图(1)表示某年12个月中每月的平均气温,图(2)表示某家庭在这年12个月中每月的用电量,根据这些信息,以下关于该家庭用电量与气温间关系的叙述中,正确的是
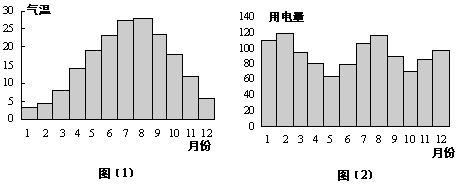
(A)气温最训时,用电量最多.
(B)气温最低时,用电量最少.
(C)当气温大于某一点一值时,用电量随气温增高而增加.
(D)当气温小于某一值时,用电量随气温降低而增加.
第Ⅱ卷
(1)若zC,且(3+z)i=1 (i为虚数单位),则z= 。
(2)已知向量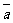 和
和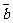 的夹角为120°,且
的夹角为120°,且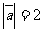 ,
,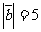 ,则
,则 = 。
= 。
(3)方程 log3(1-2·3x)=2x+1的解x= 。
(4)若正四棱锥的底面边长为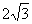 cm,体积为cm3,则它的侧面与底面所成的二面角的大小是 。
cm,体积为cm3,则它的侧面与底面所成的二面角的大小是 。
(5)二项式(1+3x)n和(2x+5)n的展开式中,各项系数之和分别记为an、bn、n是正整数,则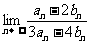 = 。
= 。
(6)已知圆x2+(y-1)2=1和圆外一点p(-2,0),过点P作圆的切线,则两条切线夹角的正切值是 。
(7)在某次花样滑冰比赛中,发生裁判受贿事件,竞赛委员会决定将裁判曰原来的9名增至14名,但只任取其中7名裁判的评分作为有效分,若14名裁判中有2人受贿,则有效分中没有受贿裁判的评分的概率是 。(结果用数值表示)
(8)抛物线(y-1)2=4(x -1)的焦点坐标是 。
(9)某工由下列工序组成,则工程总时数为 天。
|
工序 |
a |
b |
c |
d |
e |
f |
|
紧前工序 |
- |
- |
a、b |
c |
c |
d、e |
|
工时数(天) |
2 |
3 |
2 |
5 |
4 |
1 |
(10)设函数f(x)-sin2x,若f(x+t)是偶函数,则t的一个可能值是 。
(11)若数列{an}中,a1=3,且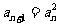 (n是正整数),则数列的通项an= 。
(n是正整数),则数列的通项an= 。
(12)已知函数y=f(x)(定义域为D,值域为A)有反函数y=f--1(x),则方程f(x)=0有解x=a,且f(x)>x(x∈D)的充要条件是y=f--1(x)满足 .
(17)(本小题满分12分)
解不等式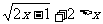 .
.
(18)(本小题满分12分)
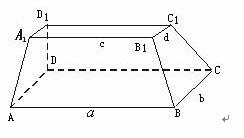
如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,上、下底面矩形的长、宽分别为c,d与a,b且a>c,b>d,两底面间的距离为h..
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角正切值;
(Ⅱ)在估测该多面体的体积时,经常运用近似公式
V估=S中截面·h来计算.已知它的体积公式是
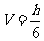 (S上底面+4S中截面+S下底面),
(S上底面+4S中截面+S下底面),
试判断V估与V的大小关系,并加以证明.
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面.)
(19)(本小题满分12分)
数列{xn}由下列条件确定: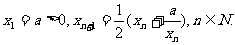
(Ⅰ)证明:对n≥2,总有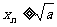 ;
;
(Ⅱ)证明:对n≥2,总有 ;
;
(20)(本小题满分12分)
在研究并行计算的基本算法时,有以下简单模型问题:
用计算机求n个不同的数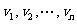 的和
的和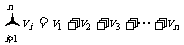 .计算开始前,n个数存贮在n台由网络连接的计算机中,每台机器存一个数,计算开始后,在一个单位时间内,每台机器至多到一台其他机器中读数据,并与自己原有数据相加得到新的数据,各台机器可同时完成上述工作.
.计算开始前,n个数存贮在n台由网络连接的计算机中,每台机器存一个数,计算开始后,在一个单位时间内,每台机器至多到一台其他机器中读数据,并与自己原有数据相加得到新的数据,各台机器可同时完成上述工作.
为了用尽可能少的单位时间,使各台机器都得到这n个数的和,需要设计一种读和加的方法.比如n=2时,一个单位时间即可完成计算,方法可用下表表示:
|
机器号 |
初始时 |
第一单位时间 |
第二单位时间 |
第三单位时间 |
|||
|
|
|
被读机号 |
结 果 |
被读机号 |
结 果 |
被读机号 |
结 果 |
|
1 |
v1 |
2 |
v1+ v2 |
|
|
|
|
|
2 |
v2 |
1 |
v2+v1 |
|
|
|
|
(Ⅰ)当n=4时,至少需要多少个单位时间可完成计算?
把你设计的方法填入下表
|
机器号 |
初始时 |
第一单位时间 |
第二单位时间 |
第三单位时间 |
|||
|
|
|
被读机号 |
结 果 |
被读机号 |
结 果 |
被读机号 |
结 果 |
|
1 |
v1 |
|
|
|
|
|
|
|
2 |
v2 |
|
|
|
|
|
|
|
3 |
v3 |
|
|
|
|
|
|
|
4 |
v4 |
|
|
|
|
|
|
(Ⅱ)当n=128时,要使所有机器都得到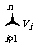 ,至少需要多少个单位时间可完成计算?(结论不要求证明)
,至少需要多少个单位时间可完成计算?(结论不要求证明)
(21)(本小题满分13分)
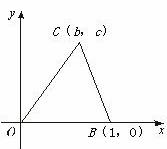
已知O(0,0),B(1,0),C(b,c)是△OBC的三个顶点.
(Ⅰ)写出△OBC的重心G,外心F,垂心H的坐标,并证明G,F,H三点共线;
(Ⅱ)当直线FH与OB平行时,求顶点C的轨迹.
(22)(本小题满分13分)
已知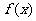 是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:
是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:
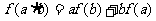 .
.
(Ⅰ)求f(0),f(1)的值;
(Ⅱ)判断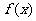 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(Ⅲ)若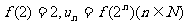 ,求证
,求证 .
.
(13)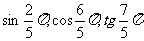 从小到大的顺序是
.
从小到大的顺序是
.
(14)等差数列{an}中,a1=2,公差不为零,且a1,a3,a11恰好是某等比数列的前三项,那么该等比数列公比的值等于 .
(15)关于直角AOB在定平面α内的射影有如下判断:①可能是0°的角;②可能是锐角;③可能是直角;④可能是钝角;⑤可能是180°的角.其中正确判断的序号是
(注:把你认为是正确判断的序号都填上).
(16)圆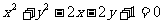 的动点Q到直线
的动点Q到直线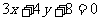 距离的最小值为 .
距离的最小值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com