
(17)(本小题满分12分)
已知函数f(x)=sin2x+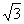 xcosx+2cos2x,x
xcosx+2cos2x,x R.
R.
(I)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)函数f(x)的图像可以由函数y=sin2x(x∈R)的图像经过怎样的变换得到?
(18)(本小题满分12分)
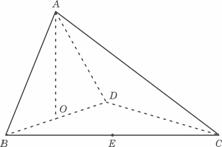
如图,四面体ABCD中,O、E分别BD、BC的中点,CA=CB=CD=BD=2
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的大小;
(Ⅲ)求点E到平面的距离.
(19)(本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=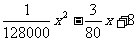 (0<x≤120).已知甲、乙两地相距100千米。
(0<x≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(20)(本小题满分12分)
已知椭圆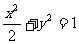 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
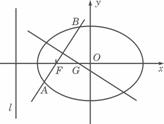
(Ⅰ)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(Ⅱ)设过点F且不与坐标轴垂直交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
(21)(本小题满分12分)
已知函数f(x)=-x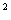 +8x,g(x)=6lnx+m
+8x,g(x)=6lnx+m
(Ⅰ)求f(x)在区间[t,t+1]上的最大值h(t);
(Ⅱ)是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;,若不存在,说明理由。
(22)(本小题满分14分)
已知数列{a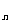 }满足a
}满足a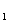 =1,a
=1,a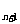 =2a
=2a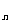 +1(n∈N
+1(n∈N )
)
(Ⅰ)求数列{a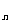 }的通项公式;
}的通项公式;
(Ⅱ)若数列{bn}满足4k1-14k2-1…4k-1=(an+1)km(n∈N*),证明:{bn}是等差数列;
(Ⅲ)证明: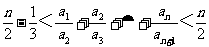 (n∈N*).
(n∈N*).
(13)(x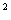 -
-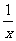 )
)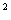 展开式中x
展开式中x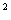 的系数是
(用数字作答)
的系数是
(用数字作答)
(14)已知直线x-y-1=0与抛物线y=ax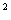 相切,则a=
相切,则a=
(15)一个均匀小正方体的六个面中,三个面上标以数0,两个面上标以数1,一个面上标以数2,将这个小正方体抛掷2次,则向上的数之积的数学期望是
(16)如图,连结△ABC的各边中点得到一个新的△A1B1C1,又连结的△A1B1C1各边中点得到,如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,…,这一系列三角形趋向于一个点M,已知A(0,0) ,B(3,0),C(2,2),则点M的坐标是 .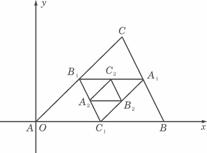
(1)设a、b、c、d∈R,则复数(a+bi)(c+di)为实数的充要条件是
A.ad-bc=0 B.ac-bd=0 C. ac+bd=0 D.ad+bc=0
(2)在等差数列{a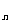 }中,已知a
}中,已知a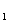 =2,a
=2,a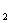 +a
+a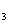 =13,则a
=13,则a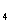 +a
+a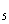 +a
+a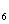 等于
等于
A.40 B.42 C.43 D.45
(3)已知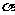 ∈(
∈(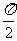 ,
,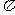 ),sin
),sin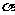 =
=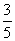 ,则tan(
,则tan(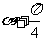 )等于
)等于
A.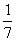 B.7
C.-
B.7
C.- 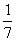 D.-7
D.-7
(4)已知全集U=R,且A={x︱︱x-1︱>2},B={x︱x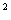 -6x+8<0},则(
-6x+8<0},则(
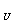 A)∩等于
A)∩等于
A.[-1,4] B. (2,3) C. (2,3) D.(-1,4)
(5)已知正方体外接球的体积是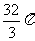 ,那么正方体的棱长等于
,那么正方体的棱长等于
A.2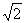 B.
B.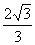 C.
C.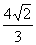 D.
D.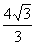
(6)在一个口袋中装有5个白球和3个黑球,这些球除颜色外完全相同,从中摸出3个球,至少摸到2个黑球的概率等于
A.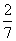 B.
B.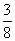 C.
C.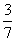 D.
D.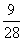
(7)对于平面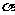 和共面的直线m、n,下列命题中真命题是
和共面的直线m、n,下列命题中真命题是
A.若m⊥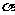 ,m⊥n,则n∥
,m⊥n,则n∥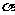 B.若m∥
B.若m∥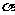 ,n∥
,n∥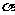 ,则m∥n
,则m∥n
C.若m
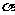 ,n∥
,n∥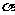 ,则m∥n
D.若m、n与
,则m∥n
D.若m、n与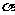 所成的角相等,则n∥m
所成的角相等,则n∥m
(8)函数y=㏒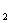
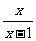 (x﹥1)的反函数是
(x﹥1)的反函数是
A.y=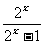 (x>0)
B.y=
(x>0)
B.y=
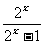 (x<0)
(x<0)
C.y=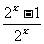 (x>0) D. .y=
(x>0) D. .y=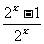 (x<0)
(x<0)
(9)已知函数f(x)=2sin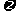 x(
x(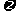 >0)在区间[
>0)在区间[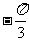 ,
,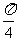 ]上的最小值是-2,则
]上的最小值是-2,则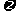 的最小值等于
的最小值等于
A.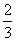 B.
B.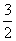 C.2
D.3
C.2
D.3
(10)已知双曲线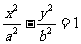 (a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
(a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
A.( 1,2) B. (1,2) C.[2,+∞] D.(2,+∞)
(11)已知︱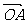 ︱=1,︱
︱=1,︱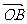 ︱=
︱=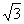 ,
,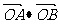 =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设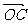 =m
=m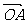 +n
+n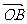 (m、n∈R),则
(m、n∈R),则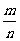 等于
等于
A.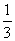 B.3
C.
B.3
C.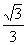 D.
D.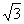
(12)对于直角坐标平面内的任意两点A(x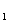 ,
, y
y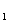 )、B(x
)、B(x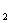 ,y
,y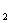 ),定义它们之间的一种“距离”:‖AB‖=︱x
),定义它们之间的一种“距离”:‖AB‖=︱x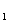 -x
-x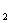 ︱+︱y
︱+︱y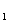 -y
-y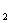 ︱.
︱.
给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖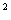 +‖CB‖
+‖CB‖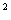 =‖AB‖
=‖AB‖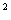 ;
;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题的个数为
A.0 B.1 C.2 D.3
第Ⅱ卷
(15)(本小题共12分)已知函数f(x)=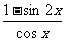 (Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tan
(Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tan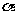 =
=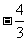 ,求f(
,求f(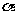 )的值.
)的值.
(16)(本小题共13分)
已知函数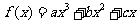 在点
在点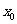 处取得极大值
处取得极大值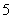 ,其导函数
,其导函数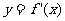 的图像经过点
的图像经过点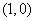 ,
,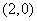 ,如图所示.求:
,如图所示.求:
(Ⅰ)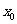 的值;
的值;
(Ⅱ)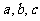 的值.
的值.
(17)(本小题共14分)
如图,ABCD-A1B1C1D1是正四棱柱.
(Ⅰ)求证:BD⊥平面ACC1A1;
(Ⅱ)若二面角C1-BD-C的大小为60o,求异面直线BC1与AC所成角的大小.
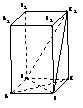
(18)(本小题共13分)
某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
(19)(本小题共14分)
椭圆C: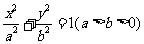 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且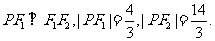
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l过圆x2+y2+4x-2y=0的圆心,交椭圆C于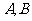 两点,且A、B关于点M对称,求直线l的方程.
两点,且A、B关于点M对称,求直线l的方程.
(20)(本小题共14分)
设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(Ⅰ)若a11=0,S14=98,求数列{an}的通项公式;
(Ⅱ)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式.
(9)若三点A(2,2),B(a,0),C(0,4)共线,则a的值等于 。
(10)在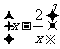 的展开式中,x3的系数是
.(用数字作答)
的展开式中,x3的系数是
.(用数字作答)
(11)已知函数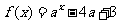 的反函数的图像经过点(-1,2),那么a的值等于
.
的反函数的图像经过点(-1,2),那么a的值等于
.
(12)已知向量a=(cos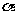 ,sin
,sin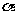 ),b=(cos
),b=(cos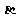 ,sin
,sin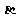 ),且a
),且a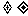 b,那么a+b与a-b的夹角的大小是
.
b,那么a+b与a-b的夹角的大小是
.
(13)在△ABC中, A,
A, B,
B, C所对的边长分别为a,b,c.若sinA:sinB:sinC=5∶7∶8,则a∶b∶c=
,
C所对的边长分别为a,b,c.若sinA:sinB:sinC=5∶7∶8,则a∶b∶c=
,  B的大小是
.
B的大小是
.
(14) 已知点P(x,y)的坐标满足条件 点O为坐标原点,那么|PO|的最小值等于____________,最大值等于______________.
点O为坐标原点,那么|PO|的最小值等于____________,最大值等于______________.
(1)设集合A=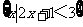 ,B=
,B=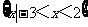 ,则A
,则A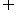 B等于
B等于
(A) 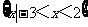 (B)
(B)
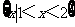 (C)
(C) 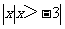 (D)
(D) 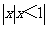
(2)函数y=1+cosx的图像
(A)关于x轴对称 (B)关于y轴对称
(C)关于原点对称 (D)关于直线x=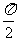 对称
对称
(3)若a与b-c都是非零向量,则“a·b=a·c”是“a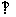 (b-c)”的
(b-c)”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D) 既不充分也不必要条件
(4)在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有
(A)36个 (B)24个 (C)18个 (D)6个
(5)已知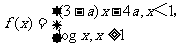 是(-
是(- ,+
,+ )上的增函数,那么a的取值范围是
)上的增函数,那么a的取值范围是
(A)(1,+ ) (B)(-
) (B)(- ,3) (C)
,3) (C)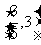 (D)(1,3)
(D)(1,3)
(6)如果-1,a,b,c,-9成等比数列,那么
(A)b=3,ac=9 (B)b=-3,ac=9 (C)b=3,ac=-9 (D)b=-3,ac=-9
(7)设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是
(A)若AC与BD共面,则AD与BC共面
(B)若AC与BD是异面直线,则AD与BC是异面直线
(C) 若AB=AC,DB=DC,则AD=BC
(D) 若AB=AC,DB=DC,则AD 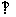 BC
BC
(8)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口A、B、C的机动车辆数如图所示,图中x1`x2`x3,分别表示该时段单位时间通过路段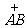 ,
,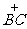 ,
, 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
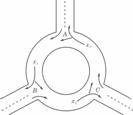
(A)x1>x2>x3 (B)x1>x3>x2 (C)x2>x3>x1 (D)x3>x2>x1
第Ⅱ卷
(15)(本小题共 12 分)
已知函数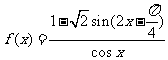 .
.
(Ⅰ)求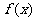 的定义域;
的定义域;
(Ⅱ)设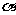 的第四象限的角,且
的第四象限的角,且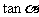
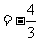 ,求
,求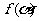 的值
的值
(16)(本小题共 13 分)
已知函数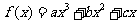 在点
在点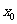 处取得极大值5,其导函数
处取得极大值5,其导函数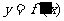
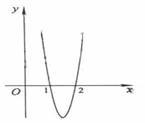
的图像经过点(1,0),(2,0),如图所示,求:(Ⅰ)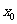 的值; (Ⅱ)a,b,c 的值.
的值; (Ⅱ)a,b,c 的值.
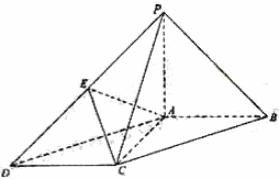
(17)(本小题共 14 分)
如图,在底面为平行四边形的四棱锥 P-ABCD 中,AB⊥AC,PA⊥平面 ABCD,且 PA=PB,点 E 是 PD 的中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB//平面 AEC;
(Ⅲ)求二面角 E-AC-B 的大小.
(18)(本小题共 13 分)
某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是 a,b,c,且三门课程考试是否及格相互之间没有影响. 求:
(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率;
(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小.(说明理由)
(19)(本小题共 14 分)
已知点 M(-2,0),N(2,0),动点 P满足条件|PM |-|PN |=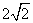 ,记动点 P的轨 迹为 W.
,记动点 P的轨 迹为 W.
(Ⅰ)求 W 的方程;
(Ⅱ)若 A,B 是W上的不同两点,O 是坐标原点,求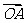 、
、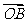 的最小值.
的最小值.
(20)(本小题共 14 分)
在数列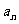 中,若 a1,a2 是正整数,且
中,若 a1,a2 是正整数,且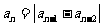 ,
,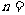 3,4,5,…,则称
3,4,5,…,则称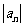 为“绝对差数列”.
为“绝对差数列”.
(Ⅰ)举出一个前五项不为零的“绝对差数列”(只要求写出前十项);
(Ⅱ)若“绝对差数列”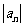 中,
中,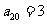 ,
,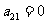 ,数列
,数列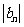 满足
满足 n=1,2,3,…,分虽判断当
n=1,2,3,…,分虽判断当 时,
时, 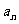 与
与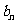 的极限是否存在,如果存在,求出其极限值;
的极限是否存在,如果存在,求出其极限值;
(Ⅲ)证明:任何“绝对差数列”中总含有无穷多个为零的项.
(9)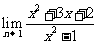 的值等于
的值等于 .
(10)在
.
(10)在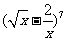 的展开式中,
的展开式中, 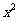 的系数是
的系数是 .(用数字作答)
.(用数字作答)
(11)若三点 A(2,2),B(a,0),C(0,b)(0 ,b)(ab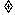 0)共线,则,
0)共线,则, 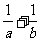 的值等于
的值等于
(12)在△ABC 中,若 C B A sin A: sinB: sinC =5:7:8. 则∠B 的大小是 (13)已知点 P(x,y)的坐标满足条件
(13)已知点 P(x,y)的坐标满足条件 点O为坐标原点,那么|PO |的最小值
点O为坐标原点,那么|PO |的最小值
等于 ,最大值等于
,最大值等于 .
.
(14)已知A、B、C三点在球心为 O,半径为R 的球面上,AC⊥BC,且 AB=R,那么 A、B 两点间的球面距离为 球心到平面 ABC 的距离为
球心到平面 ABC 的距离为 .
.
(1)在复平面内,复数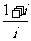 对应的点位于
对应的点位于
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
(2)若 a 与 b-c 都是非零向量,则“a·b=a·c”是“a⊥(b-c)”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(3)在 1,2,3,4,5 这五个数字组成的没有重复数字的三位数中,各位数字之和为
(A)36 个 (B)24 个
(C)18 个 (D)6 个
(4)平面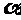 的斜线 AB 交
的斜线 AB 交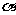 于点 B,过定点 A 的动直线
于点 B,过定点 A 的动直线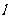 与 AB 垂直,且交
与 AB 垂直,且交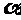 于点 C,则动 点 C 的轨迹是
于点 C,则动 点 C 的轨迹是
(A)一条直线 (B)一个圆 (C)一个椭圆 (D)双曲线的一支
(5)已知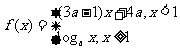 是
是 上的增函数,那么 a 的取值范围是
上的增函数,那么 a 的取值范围是
(A)(0,1) (B)(0,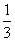 ) (C)
) (C) ,
,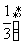 (D)
(D)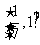
(6)在下列四个函数中,满足性质:“对于区间(1,2)上的任意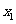 ,
,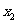 (
(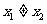 ).
).
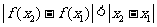 恒成立”的只有
恒成立”的只有
(A)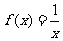 (B)
(B)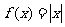
(C)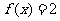 (D)
(D)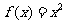
(7)设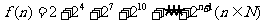 ,则
,则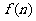 等于
等于
(A)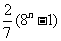 (B)
(B)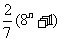
(C)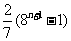 (D)
(D)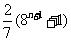
(8)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 A、B、
C 的机动车辆数如图所示,图中 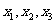 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段 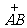 ,
,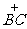
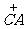 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A)
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A) 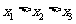
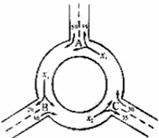 (B)
(B) 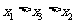
(C)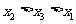
(D)
(D)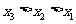
第 II 卷
(17)(本大题满分12分)已知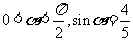
(Ⅰ)求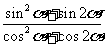 的值;
的值;
(Ⅱ)求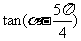 的值。
的值。
(18)(本大题满分12分)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。
(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率;
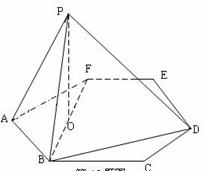
(19)(本大题满分12分)如图,P是边长为1的正六边形ABCDEF所在平面外一点,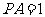 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明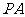 ⊥
⊥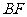 ;
;
(Ⅱ)求面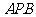 与面
与面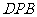 所成二面角的大小。
所成二面角的大小。
(20)(本大题满分12分)设函数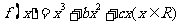 ,已知
,已知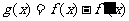 是奇函数。
是奇函数。
(Ⅰ)求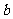 、
、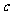 的值。
的值。
(Ⅱ)求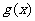 的单调区间与极值。
的单调区间与极值。
(21)(本大题满分12分)在等差数列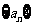 中,
中,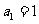 ,前
,前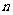 项和
项和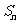 满足条件
满足条件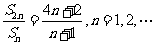 ,
,
(Ⅰ)求数列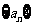 的通项公式;
的通项公式;
(Ⅱ)记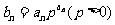 ,求数列
,求数列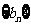 的前
的前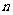 项和
项和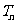 。
。
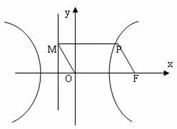
(22)(本大题满分14分)如图,F为双曲线C: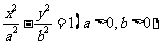 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于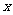 轴上方,M为左准线上一点,
轴上方,M为左准线上一点,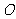 为坐标原点。已知四边形
为坐标原点。已知四边形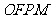 为平行四边形,
为平行四边形,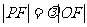 。
。
(Ⅰ)写出双曲线C的离心率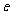 与
与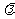 的关系式;
的关系式;
(Ⅱ)当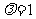 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若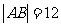 ,求此时的双曲线方程。
,求此时的双曲线方程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com