
18、(本小题满分14分)已知f(x)=ax2-c,-4≤f(1)≤-1,-1≤f(2)≤5,试求f(3)的取值范围。
17、(本小题满分12分)已知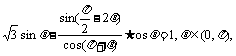 求θ的值.
求θ的值.
16、已知i,
j为互相垂直的单位向量,a = i – 2j, b = – i + λj,且a与b的夹角为钝角,则实数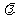 的取值范围是 ▲
.
的取值范围是 ▲
.
15、在直线y=-2上有一点P,它到A(-3,1)和B(5,-1)的距离之和最小,则P点的坐标为 ▲ .
13、 给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线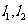 与同一平面所成的角相等,则
与同一平面所成的角相等,则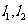 互相平行.
互相平行.
④若直线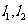 是异面直线,则与
是异面直线,则与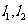 都相交的两条直线是异面直线.
都相交的两条直线是异面直线.
其中真命题的个数是 ▲ 。
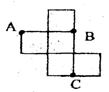 14、如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个顶点,则在正方体
14、如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个顶点,则在正方体
盒子中,∠ABC等于 ▲ .
12、已知a,b,c成等差数列(a,b,c互不相等),则二次函数y=ax2+2bx+c的图象与x轴交点个数是 ▲ 。
11、已知点P(x,y)的坐标满足条件 点O为坐标原点,那么|PO|的最大值等于▲ 。
点O为坐标原点,那么|PO|的最大值等于▲ 。
10、若圆(x-3)2+(y+5)2=r2上有且只有两个点到直线4x-3y-2=0距离等于1,则半径r取值范围是
A、[4,6] B、[4,6) C、(4,6] D、(4,6)
9、已知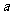 ,
,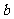 是两条直线,
是两条直线,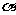 ,
,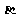 是两个平面,有下列4个命题:
是两个平面,有下列4个命题:
①若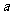 //
//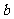 ,
, ,则
,则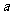 //
//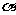
②若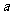 ⊥
⊥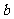 ,
,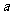 ⊥
⊥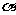 ,
,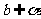 ,则
,则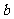 //
//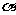
③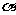 ⊥β,
⊥β,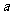 ⊥
⊥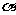 ,
,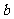 ⊥β,则
⊥β,则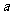 ⊥
⊥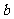
④若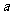 ,
,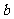 异面,
异面,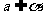 ,
, ,
,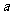 //β,则
//β,则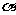 //β
//β
其中正确命题有
A、①② B、②③ C、③④ D、②④
8、 对于函数f(x)=ax2+bx+c(a≠0),若作代换x=g(t),则不改变函数f(x)的值域的代换是
A、g(t)=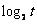 B、g(t)=|t|
C、g(t)=cost
D、g(t)=
B、g(t)=|t|
C、g(t)=cost
D、g(t)=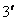
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com