1．　 若集合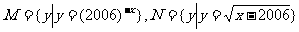，则=　　　　　　　　 。

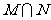22．(本小题满分14分)已知圆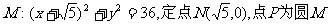上的动点，点Q在NP上，点G在MP上，且满足.

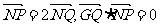　 (1)求点G的轨迹C的方程；　

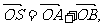　 (2)过点(2，0)作直线，与曲线C交于A、B两点，O是坐标原点，设 是否存在这样的直线，使四边形OASB的对角线相等(即|OS|=|AB|)？若存在，求出直线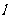的方程；若不存在，试说明理由.

21. (本题满分12分)对于数列{a_n}，定义{△a_n }为数列{a_n}的一阶差分数列，其中

(1)若数列{a_n}的通项公式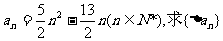的通项公式；

(2)若数列{a_n}的首项是1，且满足，

①证明数列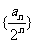为等差为数列；　 ②求{a_n}的前n项和S_n

20．(本题满分12分)已知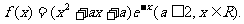

　 (1)当a=1时，求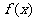的单调区间；

　 (2)是否存在实数a，使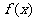的极大值为3？若存在，求出a的值，若不存在，说明理由.

19. (本题满分12分)如图，四棱锥P-ABCD的底面是AB=2，BC=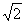的矩形，侧面PAB

是等边三角形，且侧面PAB⊥底面ABCD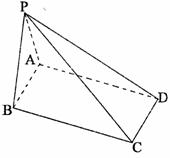　　　 　　

(Ⅰ)证明：侧面PAB⊥侧面PBC； (II)求侧棱PC与底面ABCD所成的角；

(III)求直线AB与平面PCD的距离．

18.(本题满分12分)已知函数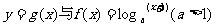的图象关于原点对称.

(1)写出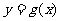的解析式；(2)若函数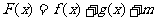为奇函数，试确定

实数m的值； (3)当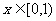时，总有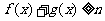成立，求实数n的取值范围.

17．(本小题满分12分)若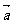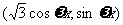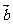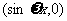＝，＝,其中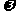>0,记函数f(x)=(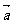+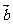)·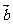+k．(1)若f(x)图象中相邻两条对称轴间的距离不小于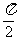，求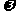的取值范围．　　 (2)若f(x)的最小正周期为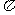，且当x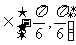时，f(x)的最大值是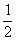，求f(x)的解析式，

16.令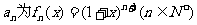的展开式中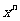项的系数，则数列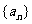的前n项和为　　　 .

15．如图：正方形ABCD所在平面与正方形ABEF所在平面成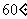的二面角，则异面直线AD与BF所成角的余弦值是______________________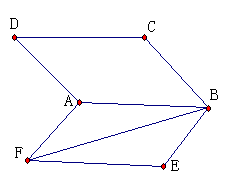

14．过双曲线x²－y²＝4上任一点M(x₀,y₀)作它的一条渐近线的垂线段，垂足为N，O为坐标原点，则△MON的面积是　　　　 .