
21. (本题满分16分,其中第(1)小题8分,第(2)小题8分)已知存在实数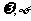 (其中
(其中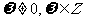 )使得函数
)使得函数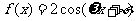 是奇函数,且在
是奇函数,且在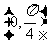 上是增函数。
上是增函数。
(1) 试用观察法猜出两组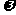 与
与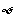 的值,并验证其符合题意;
的值,并验证其符合题意;
(2) 求出所有符合题意的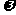 与
与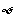 的值。
的值。
20. (本题满分14分,第(1)小题6分,(2)小题8分)在平面直角坐标系中,若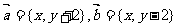 ,且
,且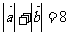 。
。
(1) 求动点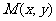 的轨迹C的方程;
的轨迹C的方程;
(2) 过点(0,3)作直线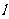 与曲线C交于A、B两点,设
与曲线C交于A、B两点,设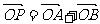 ,是否存在这样的直线
,是否存在这样的直线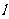 ,使得四边形OAPB为矩形?若存在,求出直线
,使得四边形OAPB为矩形?若存在,求出直线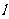 的方程,不存在,说明理由。
的方程,不存在,说明理由。
19. (本题满分14分,第(1)小题6分,(2)小题8分)设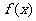 是
是 上的奇函数,对任意实数x,都有
上的奇函数,对任意实数x,都有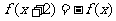 ,当
,当 时,
时,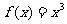 。
。
(1) 试证: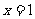 是函数
是函数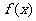 的一条对称轴;
的一条对称轴;
(2) 证明函数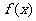 是以4为周期的函数,并求
是以4为周期的函数,并求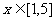 时,
时,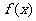 的解析式。
的解析式。
18.(本题满分12分,第(1)6分,第(2)6分)某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如ΔDQH等)上铺草坪,造价为80元/m2。
(1) 设总造价为S元,AD长为xm,试建立S与x的函数关系;
(2) 当x为何值时,S最小?并求这个最小值。
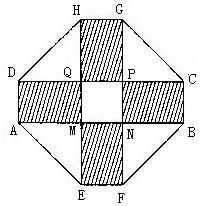
第18题图
17.(本题满分12分)已知x∈R,z∈C,x,z满足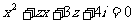 。
。
(1) 若z在复平面内对应的点Z在第一象限,求x的范围;
(2) 是否存在这样x,使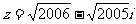 成立。
成立。
16.在ΔABC中,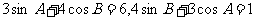 ,则C等于( )
,则C等于( )
A.300 B.1500 C.300或1500 D.600或1200
15.如图,OA是双曲线实半轴,OB是虚半轴,F是焦点,且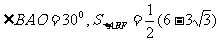 ,则双曲线的方程是( )
,则双曲线的方程是( )
 y
y

 B
B
 O A F x
O A F x
第15题图
A.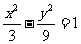 B.
B.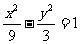 C.
C.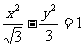 D.
D.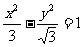
14.直线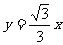 绕原点逆时针方向旋转300后,所得直线与圆
绕原点逆时针方向旋转300后,所得直线与圆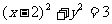 的位置关系是( )。
的位置关系是( )。
A.直线过圆心 B.直线与圆相交,但不过圆心
C.直线与圆相切 D.直线与圆没有公共点
13.设A、B是锐角三角形的两个内角,则复数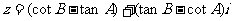 对应点位于复平面的( )。
对应点位于复平面的( )。
A. 第一象限 B.第二象限 C.第三象限 D.第四象限
12.若 ,则
,则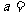 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com