
7. 定义:称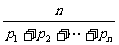 为n个正数
为n个正数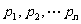 的“均倒数”,若数列{
的“均倒数”,若数列{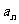 }的前n项的“均倒数”为
}的前n项的“均倒数”为 ,则数列{
,则数列{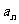 }的通项公式为( )
}的通项公式为( )
(A). 2n-1 ( B). 4n-1 (C). 4n-3 ( D). 4n-5
6.已知函数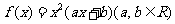 在
在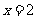 时有极值,其图象在点
时有极值,其图象在点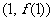 处的切线与直线
处的切线与直线 平行,则函数
平行,则函数 的单调减区间为( )
的单调减区间为( )
(A).(-∞,0) (B).(0,2)
(C).(2,+∞) (D).(-∞,+∞)
5.已知 是实数集 R上的奇函数,且在区间
是实数集 R上的奇函数,且在区间 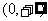 上单调递增,若
上单调递增,若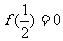 ,
, 的内角A 满足
的内角A 满足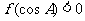 ,则A的取值范围是( )
,则A的取值范围是( )
(A)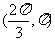 (B)
(B)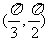 (C)
(C) (D)
(D)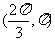
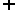
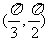
4.设向量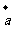 =(1,-3),
=(1,-3), =(-2,4),
=(-2,4),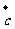 =(-1,-2),若表示向量4
=(-1,-2),若表示向量4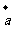 、4
、4 -2
-2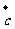 、2
、2 、
、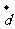 的有向线段首尾相接能构成四边形,则向量
的有向线段首尾相接能构成四边形,则向量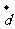 为( )
为( )
(A)(2,6); (B)(-2,6); (C)(2,-6); (D)(-2,-6).
3.设 =
=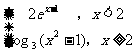 ,则不等式
,则不等式 >2的解集为( )
>2的解集为( )
(A)(1,2)∪(3,+∞); (B)(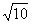 ,+∞);
,+∞);
(C)(1,2)∪(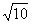 ,+∞); (D)(1,2).
,+∞); (D)(1,2).
2.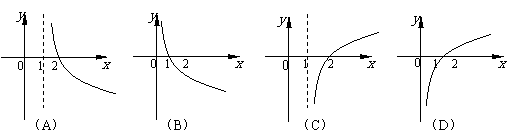 函数
函数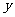 =1+
=1+ (0<
(0<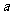 <1)的反函数的图象大致是(
)
<1)的反函数的图象大致是(
)
1.定义集合运算:A◇B=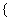
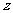 |
|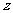 =
=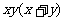 ,
,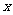 ∈A,
∈A,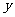 ∈B
∈B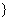 ,设集合A=
,设集合A=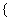 0,1
0,1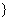 ,
,
B=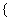 2,3
2,3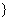 ,则集合A◇B的所有元素之和为(
)
,则集合A◇B的所有元素之和为(
)
(A)0; (B)6; (C)12; (D)18.
20.
(本小题满分14分)已知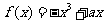 在(0,1)上是增函数。
在(0,1)上是增函数。
(I)求实数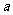 的取值的集合A;
的取值的集合A;
(II)当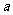 取A中的最小值时,定义数列
取A中的最小值时,定义数列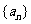 满足
满足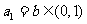 ,且
,且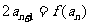
试比较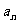 与
与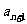 的大小?
的大小?
(III)在(II)的条件下,问是否存在正实数c,使得0<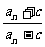 <2对于一切
<2对于一切 恒成立?若存在,求出c的取值范围;若不存在,说明理由。
恒成立?若存在,求出c的取值范围;若不存在,说明理由。
19.
(本小题满分14分)已知函数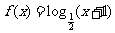 ,当点
,当点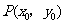 在
在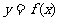 的图像上移动时,点
的图像上移动时,点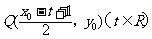 在函数
在函数 的图像上移动.
的图像上移动.
(1) 若点P坐标为(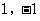 ),点Q也在
),点Q也在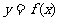 的图像上,求
的图像上,求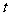 的值;
的值;
(2) 求函数 的解析式;
的解析式;
(3) 当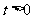 时,是否存在函数
时,是否存在函数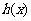 使得
使得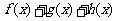 在定义域为
在定义域为
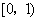 时有最小值而没有最大值?若存在,写出一个
时有最小值而没有最大值?若存在,写出一个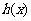 的解析式,若不存在,请说明理由.
的解析式,若不存在,请说明理由.
18.(本小题满分12分)某校为扩大教学规模,从今年起扩大招生,现有学生人数为b人,以后学生人数年增长率为4.9‰.该校今年年初有旧实验设备a套,其中需要换掉的旧设备占了一半.学校决定每年以当年年初设备数量的10%的增长率增加新设备,同时每年换掉x 套的旧设备,
(1)如果10年后该校学生的人均占有设备的比率正好比目前翻一番,那么每年应更换的旧设备是多少套?
(2)依照(1)更换速度,共需多少年能更换所有需要更换的旧设备?
下列数据供计算时参考:
|
1.19=2.38 |
1.00499=1.04 |
|
1.110=2.60 |
1.004910=1.05 |
|
1.111=2.85 |
1.004911=1.06 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com