
3.双曲线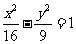 的焦点坐标为( )
的焦点坐标为( )
A.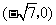 ,
,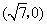 B.
B.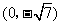 ,
,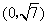
C.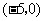 ,
,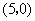 D.
D.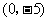 ,
,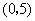
2.若函数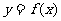 的反函数图象过点
的反函数图象过点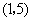 ,则函数
,则函数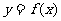 的图象必过点( )
的图象必过点( )
A.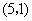 B.
B.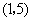 C.
C.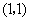 D.
D.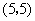
1.若集合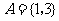 ,
,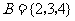 ,则
,则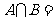 ( )
( )
A.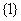 B.
B.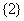 C.
C.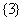 D.
D.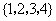
(17)(本小题满分12分)
注:此题为选做题,你可以从甲乙两题中任选一题来解,若两题都做,则只按甲题的解答来记分.
(甲)已知复数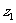 满足
满足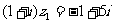 ,
, ,其中
,其中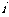 为虚数单位,
为虚数单位,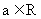 ,若
,若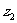 的共轭复数记为
的共轭复数记为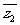 ,且
,且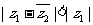 ,求
,求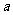 的取值范围.
的取值范围.
(乙)若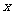 ,
,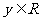 ,x>0,y>0,且x+y>2.
,x>0,y>0,且x+y>2.
求证: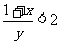 或
或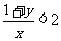 中至少有一个成立.
中至少有一个成立.
(18)(本小题满分12分)
棱长为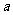 的正方体
的正方体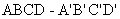 中,E、F分别是BC、A′D′的中点.求直线AD与平面B′EDF所成的角的余弦值.
中,E、F分别是BC、A′D′的中点.求直线AD与平面B′EDF所成的角的余弦值.
(19)(本小题满分12分)
已知数列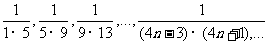
(I)计算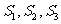
(II)根据(I)推测计算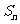 的公式,并用数学归纳法给出证明.
的公式,并用数学归纳法给出证明.
(20)(本小题满分12分)
一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为l0km/h时,燃料费是每小时6元,而其它与速度无关的费用是每小时96元,问:此轮船以多大的速度航行时,能使每千米的费用总和最少?
(21)(本小题满分12分)
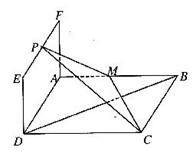
如图,平面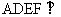 平面ABCD, ABCD与ADEF均为矩形,且
平面ABCD, ABCD与ADEF均为矩形,且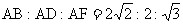 :P为线段EF上一点,M为AB中点,若PC与BD所成的角为
:P为线段EF上一点,M为AB中点,若PC与BD所成的角为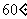 .
.
(I)试确定P点位置;
(II)求二面角P-MC-D的大小的余弦值:
(III)当AB长为多少时,点D到平面PMC的距离等于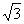 ?
?
(22)(本小题满分14分)
已知二次函数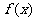 满足:(1)在
满足:(1)在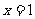 时有极值;(2)图象过点(0,-3),且在该点处的切线与直线
时有极值;(2)图象过点(0,-3),且在该点处的切线与直线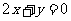 平行.
平行.
(I)求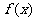 的解析式;
的解析式;
(II)设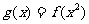 ,求
,求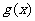 在[-1,2]上的值域;
在[-1,2]上的值域;
(III)讨论曲线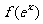 上任意两点连线的斜率恒大于
上任意两点连线的斜率恒大于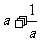 的充要条件.
的充要条件.
(13)已知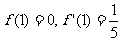 ,则
,则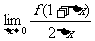 =_______________________
=_______________________
(14)已知向量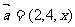 ,
,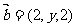 ,若
,若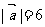 ,且
,且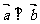 ,则
,则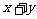 的值为________
的值为________
(15)设m,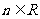 ,且
,且 是方程
是方程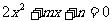 的一个根,则
的一个根,则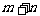 =_______
=_______
(16)在有限数列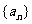 中,
中,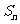 是
是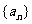 的前
的前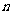 项和,若把
项和,若把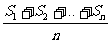 称为数列
称为数列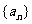 的“优化和”,现有一个共2006项的数列
的“优化和”,现有一个共2006项的数列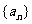 :
: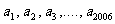 ,若其“优化和”为2007,则有2007项的数列
,若其“优化和”为2007,则有2007项的数列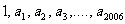 的“优化和”为__________________
的“优化和”为__________________
(1)分析法是从要证明的结论出发,逐步寻求使结论成立的 ( )
(A)充分条件 (B)必要条件 (C)充要条件 (D)等价条件
(2)曲线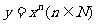 在x=2处的导数为12,则,n = ( )
在x=2处的导数为12,则,n = ( )
(A)l (B)2 (C)3 (D)4
(3)下列等于1的积分是 ( )
(A)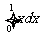 (B)
(B) 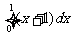 (C)
(C) 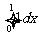 (D)
(D)
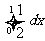
(4)下列几种推理过程是演绎推理的是 ( )
(A)某校高三l班55人,2班54人,3班52人,由此得高三所有班人数超过50人
(B)两条直线平行,同旁内角互补.如果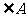 与
与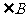 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则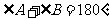
(C)在数列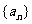 中
中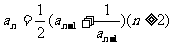 ,由此归纳
,由此归纳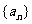 的通项公式
的通项公式
(D)由圆的周长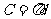 推测球的表面积
推测球的表面积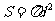
(5)满足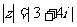 的复数z在复平面上对应的点的轨迹是 ( )
的复数z在复平面上对应的点的轨迹是 ( )
(A)一条直线 (B)圆 (C)两条直线 (D)椭圆
(6)在长方体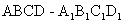 中,如果AB=BC=
中,如果AB=BC=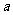 ,
,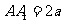 ,那么A到直线
,那么A到直线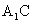 的距离等于 ( )
的距离等于 ( )
(A)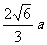 (B)
(B)
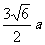 (C)
(C) 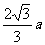 (D)
(D) 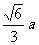
(7)描线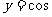 ,
,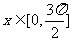 与坐标轴围成的面积是 ( )
与坐标轴围成的面积是 ( )
(A)4 (B)3 (C)2 (D)1
(8)如果向量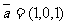 ,
,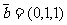 分别平行于平面
分别平行于平面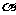 、
、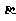 且都与此两平面的交线
且都与此两平面的交线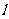 垂直,则锐二面角
垂直,则锐二面角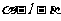 的大小是 ( )
的大小是 ( )
(A)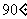 (B)
(B)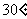 (C)
(C)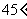 (D)
(D)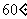
(9)已知下列求导运算:
①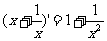
②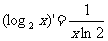
③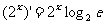
④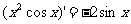
其中正确的个数是 ( )
(A)1 (B)2 (C)3 (D)4
(10)正方形ABCD中,E、F分别是AB、CD的中点,沿EF将正方形折成直二面角,则异面直线BF与DE所成角的余弦值是 ( )
(A)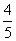 (B)
(B)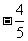
(C) 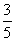 (D)
(D)
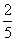
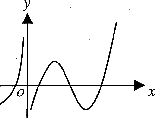
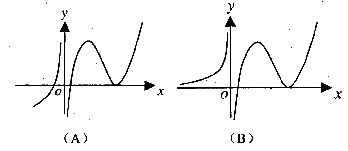
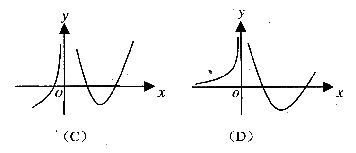
(11)设函数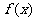 在定义域内可导,
在定义域内可导,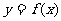 的图象如右图所示,则
的图象如右图所示,则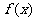 的导数
的导数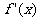 的图象大致为 ( )
的图象大致为 ( )
(12)对于R上可导的任意函数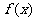 满足
满足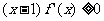 ,则必有 ( )
,则必有 ( )
(A)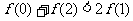 (B)
(B)
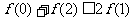
(C)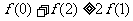 (D)
(D) 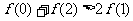
第Ⅱ卷(非选择题共90分)
l、第Ⅱ卷共7页,用钢笔或圆珠笔直接答在试题卷中。
2、答卷前将密封线内的项目填写清楚。
22.(本小题满分14分)
已知二次函数f(x)满足:(1)在x=1时有极值;(2)图象过点(0,-3),且在该点处的切线与直线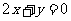 平行.
平行.
(I)求f(x)的解析式;
(II)设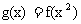 ,求g(x)在[-1,2]上的值域;
,求g(x)在[-1,2]上的值域;
(Ⅲ)讨论曲线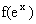 上任意一点处的切线的斜率恒大于
上任意一点处的切线的斜率恒大于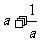 的充要条件.
的充要条件.
21.(本小题满分12分)
(Ⅰ)证明:当a>1时,不等式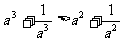 成立;
成立;
(Ⅱ)要使(Ⅰ)中不等式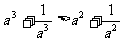 成立,能否将“a>1”这一条件适当放宽?若能,请放宽并简述理由;若不能,也请说明理由。
成立,能否将“a>1”这一条件适当放宽?若能,请放宽并简述理由;若不能,也请说明理由。
(Ⅲ)请你根据(Ⅰ)(Ⅱ)的证明,试写出一个类似的更为一般的结论,且给予证明。
20.(本小题满分12分)
一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为l0km/h时,燃料费是每小时6元,而其它与速度无关的费用每小时96元,问此轮船以多大的速度航行时,能使每千米的费用总和最少?
19.(本小题满分12分)
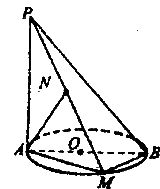
如图,AB是圆O的直径,PA垂直于圆O所在平面,M是圆周上任意一点,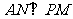 ,点N为垂足.
,点N为垂足.
求证: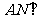 平面PBM.
平面PBM.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com