
1. 设U={a,b,c,d,e},A={b,c,d},B={b,e},则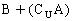 等于
等于
A. {e} B.
{a,b,e} C.
{a,b,c,d,e} D.
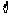
20.(本小题满分13分)
已知数列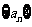 满足
满足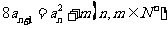 ,且
,且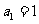 .
.
⑴ 求证:当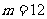 时,
时,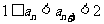 ;
;
⑵ 若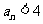 对任意的
对任意的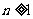 (
(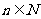 )恒成立, 求
)恒成立, 求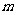 的最大值.
的最大值.
19.(本小题满分13分)
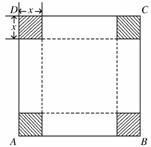
如图,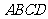 是一块边长为
是一块边长为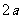 的正方形铁板,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱,若水箱的高度
的正方形铁板,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱,若水箱的高度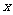 与底面边长的比不超过常数
与底面边长的比不超过常数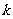
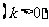 .
.
⑴ 写出水箱的容积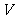 与水箱高度
与水箱高度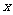 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
⑵ 当水箱高度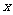 为何值时,水箱的容积
为何值时,水箱的容积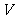 最大,并求出其最大值.
最大,并求出其最大值.
18.(本小题满分13分)
已知抛物线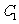 :
: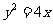 的焦点与椭圆
的焦点与椭圆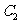 :
: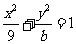 的右焦点
的右焦点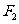 重合,
重合,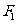 是椭圆的左焦点.
是椭圆的左焦点.
⑴ 在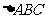 中,若
中,若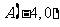 ,
,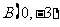 ,点
,点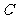 在抛物线
在抛物线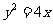 上运动,求
上运动,求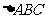 重心
重心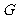 的轨迹方程;
的轨迹方程;
⑵ 若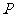 是抛物线
是抛物线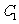 与椭圆
与椭圆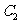 的一个公共点,且
的一个公共点,且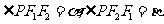 ,求
,求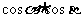 的值及
的值及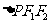 的面积.
的面积.
17.(本小题满分13分)
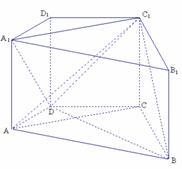
直四棱柱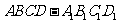 中,
中,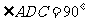 ,
,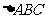 为等边三角形, 且
为等边三角形, 且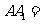
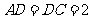 .
.
⑴ 求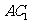 与
与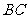 所成角的余弦值;
所成角的余弦值;
⑵ 求二面角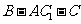 的大小;
的大小;
⑶ 设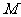 是
是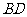 上的点,当
上的点,当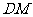 为何值时,
为何值时,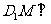 平面
平面 ?并证明你的结论.
?并证明你的结论.
16.(本小题满分13分)
已知盒子里有大小相同的球10个,其中标号为1的球3个,标号为2的球4个,标号为4的球3个.
⑴ 若从盒子里一次任取3个球,假设取出每个球的可能性都相同,求取出的三个球中标号为1,2,4的球各一个的概率;
⑵ 若第一次从盒子里任取1个球,放回后,第二次再任取1个球,假设取出每个球的可能性都相同,记第一次与第二次取出球的标号之和为 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
15.(本小题满分13分)
已知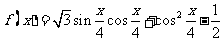 .
.
⑴ 求函数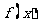 的单调递增区间;
的单调递增区间;
⑵ 在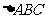 中,角
中,角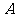 、
、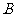 、
、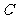 的对边分别是
的对边分别是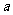 、
、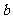 、
、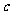 ,满足
,满足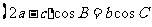 ,求函数
,求函数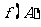 的取值范围.
的取值范围.
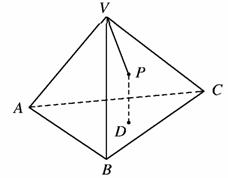
14.如图,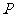 是正四面体
是正四面体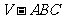 的面
的面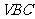 上一点,点
上一点,点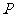 到平面
到平面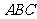 距离与到点
距离与到点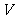 的距离相等,则动点
的距离相等,则动点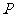 的轨迹为_______,其轨迹的离心率为_____.
的轨迹为_______,其轨迹的离心率为_____.
13.已知实数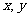 满足不等式组
满足不等式组 则
则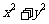 的最大值等于______,最小值等于___________.
的最大值等于______,最小值等于___________.
12.在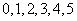 这六个数字组成的没有重复数字的五位数中,是5的倍数的共有_______个(用数字作答).
这六个数字组成的没有重复数字的五位数中,是5的倍数的共有_______个(用数字作答).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com