
1.设集合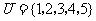 ,
,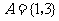 ,
,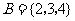 ,则
,则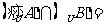 ( )
( )
A.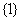 B.
B.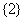 C.
C.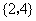 D.
D.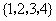
22.(本小题满分12分)
已知函数 ,
,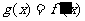 ,且对任意的实数
,且对任意的实数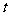 均有
均有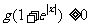 ,
,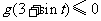 .
.
(I)求函数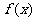 的解析式;
的解析式;
(II)若对任意的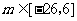 ,恒有
,恒有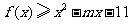 ,求
,求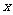 的取值范围.
的取值范围.
21.(本小题满分14分)
已知正三角形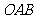 的三个顶点都在抛物线
的三个顶点都在抛物线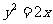 上,其中
上,其中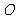 为坐标原点,设圆
为坐标原点,设圆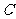 是
是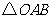 的外接圆(点
的外接圆(点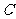 为圆心)
为圆心)
(I)求圆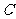 的方程;
的方程;
(II)设圆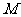 的方程为
的方程为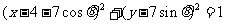 ,过圆
,过圆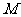 上任意一点
上任意一点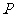 分别作圆
分别作圆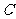 的两条切线
的两条切线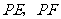 ,切点为
,切点为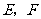 ,求
,求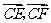 的最大值和最小值.
的最大值和最小值.
20.(本小题满分12分)
已知数列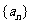 ,
,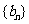 满足
满足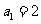 ,
,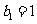 ,且
,且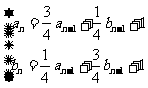 (
(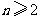 )
)
(I)令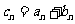 ,求数列
,求数列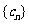 的通项公式;
的通项公式;
(II)求数列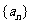 的通项公式及前
的通项公式及前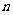 项和公式
项和公式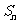 .
.
19.(本小题满分12分)
已知函数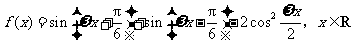 (其中
(其中 )
)
(I)求函数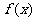 的值域;
的值域;
(II)若函数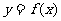 的图象与直线
的图象与直线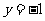 的两个相邻交点间的距离为
的两个相邻交点间的距离为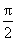 ,求函数
,求函数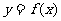 的单调增区间.
的单调增区间.
18.(本小题满分12分)
如图,在直三棱柱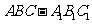 中,
中,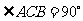 ,
,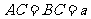 ,
,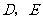 分别为棱
分别为棱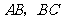 的中点,
的中点,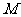 为棱
为棱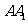 上的点,二面角
上的点,二面角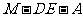 为
为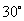 .
.
(I)证明: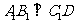 ;
;
(II)求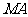 的长,并求点
的长,并求点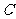 到平面
到平面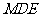 的距离.
的距离.
17.(本小题满分12分)
某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:小时)进行了统计,统计结果如下表所示:
|
分组 |
[500,900) |
[900,1100) |
[1100,1300) |
[1300,1500) |
[1500,1700) |
[1700,1900) |
[1900, ) ) |
|
频数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
|
频率 |
|
|
|
|
|
|
|
(I)将各组的频率填入表中;
(II)根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(III)该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,试求至少有2支灯管的使用寿命不足1500小时的概率.
16.设椭圆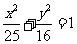 上一点
上一点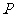 到左准线的距离为10,
到左准线的距离为10,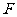 是该椭圆的左焦点,若点
是该椭圆的左焦点,若点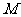 满足
满足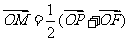 ,则
,则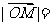 .
.
15.若一个底面边长为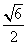 ,棱长为
,棱长为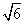 的正六棱柱的所有顶点都在一个球的面上,则此球的体积为 .
的正六棱柱的所有顶点都在一个球的面上,则此球的体积为 .
14.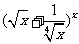 展开式中含
展开式中含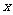 的整数次幂的项的系数之和为 (用数字作答).
的整数次幂的项的系数之和为 (用数字作答).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com