
8.设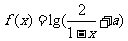 是奇函数,则使
是奇函数,则使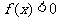 的
的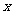 的取值范围是( )
的取值范围是( )
A.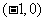 B.
B.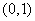
C. D.
D.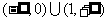
7.若对于任意实数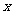 ,有
,有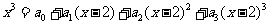 ,则
,则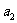 的值为( )
的值为( )
A.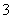 B.
B.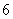 C.
C.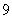 D.
D.
6.设函数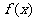 定义在实数集上,它的图像关于直线
定义在实数集上,它的图像关于直线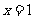 对称,且当
对称,且当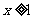 时,
时,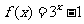 ,则有( )
,则有( )
A.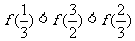 B.
B.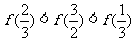
C.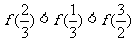 D.
D.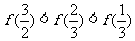
5.函数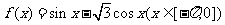 的单调递增区间是( )
的单调递增区间是( )
A.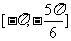 B.
B.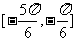 C.
C.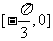 D.
D.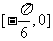
4.已知两条直线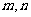 ,两个平面
,两个平面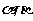 ,给出下面四个命题:
,给出下面四个命题:
①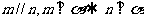 ; ②
; ②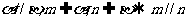 ;
;
③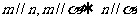 ; ④
; ④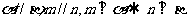 ;
;
其中正确命题的序号是( )
A.①③ B.②④ C.①④ D.②③
3.在平面直角坐标系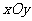 中,双曲线中心在原点,焦点在
中,双曲线中心在原点,焦点在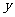 轴上,一条渐近线方程为
轴上,一条渐近线方程为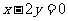 ,则它的离心率为( )
,则它的离心率为( )
A.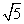 B.
B.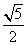 C.
C.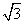 D.
D.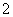
2.已知全集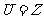 ,
,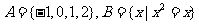 ,则
,则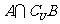 为( )
为( )
A.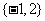 B.
B.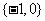 C.
C.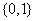 D.
D.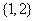
1.下列函数中,周期为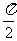 的是( )
的是( )
A.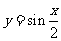 B.
B.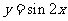 C.
C.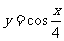 D.
D.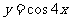
22.请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分。作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑。
A(本小题满分10分)选修4-1:几何证明选讲如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在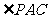 的内部,点M是BC的中点。
的内部,点M是BC的中点。
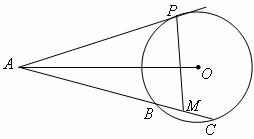
(Ⅰ)证明A,P,O,M四点共圆;
(Ⅱ)求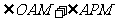 的大小。
的大小。
B(本小题满分10分)选修4-4:坐标系与参数方程
⊙O1和⊙O2的极坐标方程分别为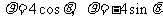 。
。
(Ⅰ)把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(Ⅱ)求经过⊙O1,⊙O2交点的直线的直角坐标方程。
C(本小题满分10分)选修4-5;不等式选讲
设函数 。
。
(Ⅰ)解不等式f(x)>2;
(Ⅱ)求函数y= f(x)的最小值。
21.(本小题满分12分)
设函数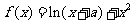
(Ⅰ)若当x=-1时,f(x)取得极值,求a的值,并讨论f(x)的单调性;
(Ⅱ)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于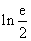 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com