
20.(本题满分14分)已知函数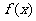 的导数
的导数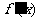 满足
满足 ,常数
,常数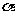 为方程
为方程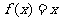 的实数根.
的实数根.
⑴.若函数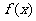 的定义域为I,对任意
的定义域为I,对任意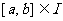 ,存在
,存在 ,使等式
,使等式 =
= 成立,求证:方程
成立,求证:方程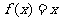 不存在异于
不存在异于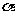 的实数根;
的实数根;
⑵.求证:当 时,总有
时,总有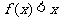 成立;
成立;
⑶.对任意 ,若满足
,若满足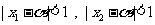 ,求证
,求证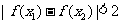 .
.
19.(本题满分14分)如图,过抛物线 的对称轴上任一点
的对称轴上任一点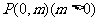 作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点.
作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点.
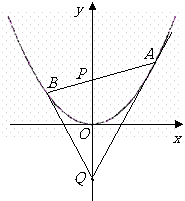

⑴.设点P满足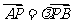 (
( 为实数),证明:
为实数),证明: ;
;
⑵.设直线AB的方程是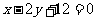 ,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
18.(本小题满分14分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,
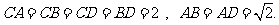
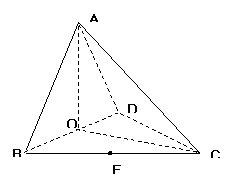

⑴.求证: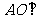 平面BCD;
平面BCD;
⑵.求异面直线AB与CD所成角余弦的大小;
⑶.求点E到平面ACD的距离.
17.(本题满分14分)已知等差数列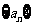 的前项和为
的前项和为 ,
,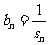 ,且
,且 ,
, .
.
⑴.求数列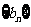 的通项公式;
的通项公式;
⑵.求证: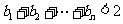 .
.
16.(本题满分12分)月饼是一种时间性很强的商品,若在中秋节前出售,每盒将获利5元,若到中秋节还没能及时售完,中秋节之后只能降价出售,每盒将亏损3元.根据市场调查,销量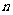 (百盒)的概率分布如下:
(百盒)的概率分布如下:
销量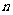 (百盒) (百盒) |
1 |
2 |
3 |
4 |
5 |
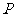 |
0.05 |
0.25 |
0.3 |
0.3 |
0.1 |
由于市场风险较大,批发商要求零售商预订月饼的数量,且每年只预订一次,订货量以百盒为单位.
⑴.设订购量为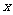 百盒时,获利额为
百盒时,获利额为 元.下表表示与
元.下表表示与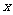 对应的
对应的 的分布列,请在空格处填入适当的
的分布列,请在空格处填入适当的 值,并计算相应的获利期望值
值,并计算相应的获利期望值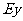 ;
;
⑵.预订多少盒月饼最合理?
 |
1 |
2 |
3 |
4 |
5 |
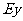 |
|
0.05 |
0.25 |
0.3 |
0.3 |
0.1 |
||
|
1 |
500 |
500 |
500 |
500 |
500 |
500 |
|
2 |
200 |
1000 |
1000 |
1000 |
1000 |
960 |
|
3 |
-100 |
700 |
1500 |
1500 |
1500 |
|
|
4 |
|
400 |
1200 |
2000 |
2000 |
|
|
5 |
|
100 |
900 |
1700 |
2500 |
|
(解答本题第⑴小题只需在下面的表格的空位中填入你认为正确的数据即可)
解:⑴.
 |
1 |
2 |
3 |
4 |
5 |
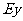 |
|
0.05 |
0.25 |
0.3 |
0.3 |
0.1 |
||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
15.(本题满分12分)已知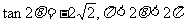 .
.
⑴求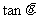 的值;⑵求
的值;⑵求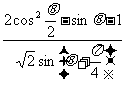 的值.
的值.
14.(本小题有三个题供选作,考生只能在①、②、③题中选做一题!多做不给分!)
①.圆C: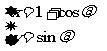 (
(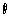 为参数)的普通方程为___________,设O为坐标原点,点
为参数)的普通方程为___________,设O为坐标原点,点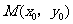 在C上运动,点
在C上运动,点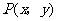 是线段OM的中点,则点P的轨迹方程为
.
是线段OM的中点,则点P的轨迹方程为
.
②.若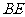 、
、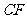 是
是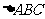 的高,且
的高,且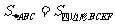 ,则
,则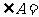 .
.
③.已知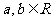 ,
,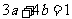 ,则
,则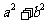 的最小值为
.
的最小值为
.
13.关于二项式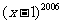 ,有下列三个命题:①.该二项式展开式中非常数项的系数和是
,有下列三个命题:①.该二项式展开式中非常数项的系数和是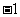 ;②.该二项式展开式中第
;②.该二项式展开式中第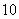 项是
项是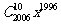 ;③.当
;③.当 时,
时,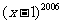 除以
除以 的余数是
的余数是 .
.
其中正确命题的序号是__________________(把你认为正确的序号都填上).
12.我们知道:“过圆为 的圆外一点
的圆外一点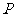 作它的两条切线
作它的两条切线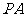 、
、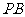 ,其中
,其中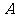 、
、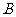 为切点,则
为切点,则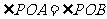 .”这个性质可以推广到所有圆锥曲线,请你写出其中一个:__________________________________________________________________________.
.”这个性质可以推广到所有圆锥曲线,请你写出其中一个:__________________________________________________________________________.
11.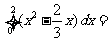 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com