
3.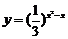 的单调递减区间是
的单调递减区间是
[课后作业]:
2.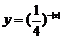 的值域是
的值域是
1.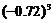 与
与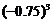 的大小关系为
的大小关系为
5.比较大小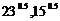 ________________.
________________.
[典型例题讲练]
例1 比较下列各组值的大小:
(1)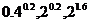 ; (2)
; (2)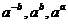 其中
其中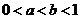 .
.
练习 比较下列各组值的大小;
(1)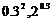 ;
(2)
;
(2)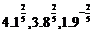 .
.
例2 已知函数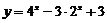 的值域为
的值域为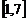 ,求
,求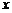 的范围.
的范围.
练习 函数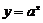 在
在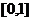 上的最大值与最小值的和为3,求
上的最大值与最小值的和为3,求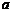 值.
值.
例3 求函数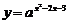 的单调减区间.
的单调减区间.
练习 函数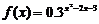 的单调减区间为 ________
.
的单调减区间为 ________
.
[课堂小结]:
[课堂检测]
4. (1)函数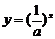 和
和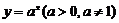 的图象关于
_ 对称.
的图象关于
_ 对称.
(2)函数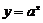 和
和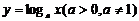 的图象关于
对称.
的图象关于
对称.
3.若函数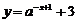 的图象恒过定点
.
的图象恒过定点
.
2.已知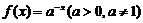 ,当
,当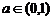 时,
时,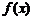 为
(填写增函数或者减函数);当
为
(填写增函数或者减函数);当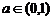 且
且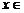 时,
时,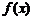 >1.
>1.
1. 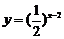 +2的定义域是_____________,值域是______________, 在定义域上,该函数单调递
+2的定义域是_____________,值域是______________, 在定义域上,该函数单调递 .
.
2.了解指数函数模型的实际案例,会用指数函数模型解决简单的实际问题
[基础知识]:
(1)一般地,函数__________________叫做指数函数,其中x是________________,函数的定义域是_______________________________.
(2)一般地,指数函数的图象与性质如下表所示:
|
|
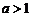 |
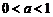 |
|
图象 |
|
|
|
定义域 |
|
|
|
值域 |
|
|
|
性质 |
(1)过定点( ) |
|
(2)当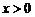 时,__________; 时,__________; 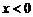 时___________. 时___________. |
(2)当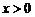 时,__________; 时,__________;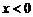 时__________. 时__________. |
|
|
(3)在( )上是______________ |
(3)在( )上是_______________ |
(3)复利公式:若某种储蓄按复利计算利息,如果本金为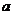 元,每期利率为
元,每期利率为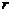 ,设存期是
,设存期是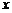 的本利和(本金+利息)为
的本利和(本金+利息)为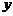 元,则
元,则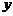 = .
= .
[基本训练]:
1.理解指数函数的概念和意义;理解指数函数的性质,会画指数函数的图象.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com