
4.函数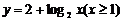 的值域是
.
的值域是
.
[典型例题讲练]
例1 求函数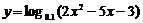 的递减区间.
的递减区间.
练习 求函数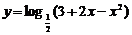 的单调区间和值域.
的单调区间和值域.
例2 已知函数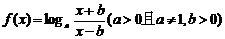 .
.
(1)求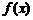 的定义域;(2)讨论
的定义域;(2)讨论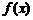 的奇偶性;(3)讨论
的奇偶性;(3)讨论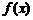 的单调性.
的单调性.
练习 求下列函数的定义域:
(1)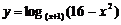 ;
(2)
;
(2)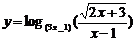 .
.
[课堂小结]熟悉对数函数的基本性质的运用
[课堂检测]
3.若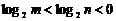 ,则实数
,则实数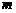 、
、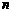 的大小关系是
.
的大小关系是
.
2.(1)函数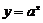 和
和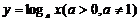 的图象关于
对称.
的图象关于
对称.
(2)函数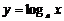 和
和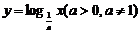 的图象关于
对称.
的图象关于
对称.
1.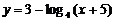 的定义域为
的定义域为 ,值域为
,值域为 .在定义域上,该函数单调递_______.
.在定义域上,该函数单调递_______.
2.对数函数的图象与性质
|
|
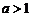 |
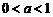 |
|
图象 |
|
|
|
定义域 |
|
|
|
值域 |
|
|
|
性质 |
(1)过定点( ) |
|
(2)当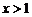 时,________________ 时,________________当 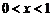 时________________ 时________________ |
(2)当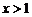 时,__________________ 时,__________________当 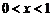 时___________________ 时___________________ |
|
|
(3)在______________是增函数 |
(3)在_____________是减函数 |
[基本训练]
2.了解指数函数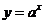 与对数函数
与对数函数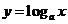 模型互为反函数(
模型互为反函数(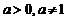 )(不要求讨论一般情形的反函数定义,也不要求求已知函数的反函数),会用指数函数模型解决简单的实际问题.
)(不要求讨论一般情形的反函数定义,也不要求求已知函数的反函数),会用指数函数模型解决简单的实际问题.
[基础知识]
1一般地,我们把函数____________叫做对数函数,其中x是自变量,函数的定义域是_______
1.了解对数函数模型的实际案例,理解对数函数的概念;理解对数函数的性质,会画指数函数的图象.
1.求下列函数的定义域和值域:
(1)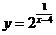 (2)
(2)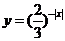 (3)
(3)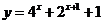
[课后作业]
1求函数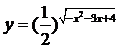 的单调区间.
的单调区间.
2求函数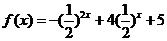 的单调区间和值域.
的单调区间和值域.
2. 设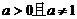 ,如果函数
,如果函数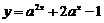 在
在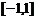 上的最大值为14,求
上的最大值为14,求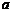 的值.
的值.
1. 指数函数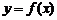 的图象经过点(
的图象经过点(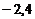 ),求
),求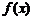 的解析式和
的解析式和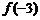 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com