
2.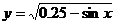 的值域是_________________
的值域是_________________
1. 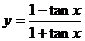 的定义域是________________
的定义域是________________
2.正弦函数、余弦函数的最小正周期T= ,公式是 ;
正切函数的最小正周期T= ,公式是
[基本训练]
1.正弦函数、余弦函数的定义域均为 ,值域可表示成[ ](有界性);正切函数的定义域为 ,值域为
2.已知函数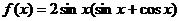
 求函数
求函数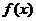 的最小正周期和最大值;
的最小正周期和最大值;
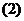 在给出的直角坐标系中,画出函数
在给出的直角坐标系中,画出函数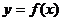 在区间
在区间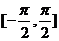 上的图象
上的图象
选做题:设函数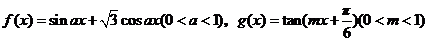
又函数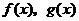 的最小正周期相同,且
的最小正周期相同,且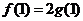 ,
,
试确定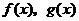 的解析式;
的解析式;
1.已知函数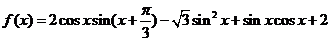 (
(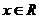 ),该函数的图象可由
),该函数的图象可由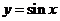 (
(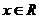 )的图象经过怎样的变换得到?
)的图象经过怎样的变换得到?
2.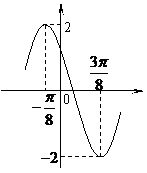 已知函数
已知函数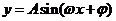 (
(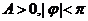 )的一段图象如下图所示,求函数的解析式.
)的一段图象如下图所示,求函数的解析式.
[课后作业]
1.若函数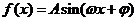 (
(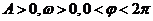 )的最小值为
)的最小值为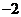 ,周期为
,周期为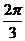 ,且它的图象过点
,且它的图象过点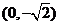 ,求此函数解析式.
,求此函数解析式.
3. 如图所示为
如图所示为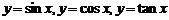 ,
,
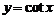 在
在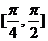 上的图象,则它们所对应的图象
上的图象,则它们所对应的图象
编号顺序是( )
A.①②③④ B.①③②④
C.③①②④ D.③①④②
§26 三角函数的图象(2)
[典型例题讲练]
例1
(1)函数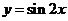 的图象向右平移
的图象向右平移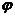 (
(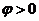 )个单位,得到的图象关于直线
)个单位,得到的图象关于直线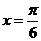 对称,则
对称,则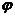 的最小值为
(2)函数
的最小值为
(2)函数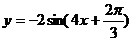 的图象与
的图象与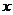 轴的交点中,离原点最近的一点是
轴的交点中,离原点最近的一点是
练习:把函数y = cos(x+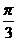 )的图象向左平移m个单位(m>0), 所得图象关于y轴对称, 则m的最小值是_________。
)的图象向左平移m个单位(m>0), 所得图象关于y轴对称, 则m的最小值是_________。
例2函数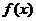 图象的一部分如图所示,则
图象的一部分如图所示,则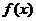 的解析式为
( )
的解析式为
( )
 A.
A.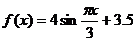
B.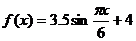
C.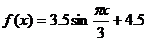

 D.
D.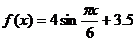
 练习:已知如图是函数
练习:已知如图是函数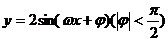 的图象,那么( )
的图象,那么( )
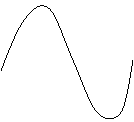 A.
A. 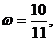
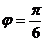
|
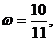
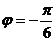
C. 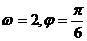
|


 D.
D. 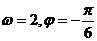
例3.设函数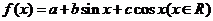 的图像过点
的图像过点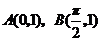 ,且b>0
,且b>0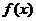 的最大值为
的最大值为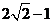 ,(1)求函数
,(1)求函数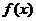 的解析式;(2)由函数y=
的解析式;(2)由函数y=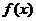 图像经过平移是否能得到一个奇函数y=
图像经过平移是否能得到一个奇函数y=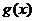 的图像?若能,请写出平移的过程;若不能,请说明理由。
的图像?若能,请写出平移的过程;若不能,请说明理由。
[课堂小结]
[课堂检测]
2.将函数 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移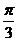 个单位,所得的图象对应的解析式是
个单位,所得的图象对应的解析式是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com