
3.不等式①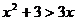 ②
②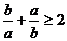 其中恒成立的是
其中恒成立的是
2.已知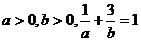 ,则
,则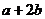 的最小值为
.
的最小值为
.
1.把长为12cm的细铁丝截成两段,各自围成一个正三角形,则这两个三角形面积之和的最小值是 .
3.已知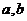 都是正数,求证:
都是正数,求证: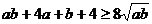
§56课题:基本不等式⑵
[典型例题讲练]
例1已知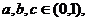 求证:
求证: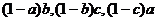 不能同时大于
不能同时大于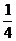 .
.
练习:已知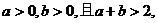 求证:
求证: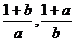 中至少有一个小于2
中至少有一个小于2
例2.已知直角三角形ABC的周长为定值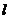 , 求这个三角形面积的最大值.
, 求这个三角形面积的最大值.
练习:已知点P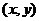 在曲线
在曲线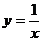 上运动,作PM垂直于
上运动,作PM垂直于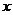 轴于点M,则△OPM(O为坐标原点)的周长的最小值是
.
轴于点M,则△OPM(O为坐标原点)的周长的最小值是
.
例3.某食品厂定期购买面粉,已知该厂每天需用面粉6吨,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨每天3元,购面粉每次需支付运费900元
(1) 求该厂多少天购买一次面粉,,才能使平均每天所支付的总费用最少?
(2) 若提供面粉的公司规定:当一次购买面粉不少于210吨时其价格可享受9折优惠(即原价的90%),问该厂是否考虑利用此优惠条件?请说明理由.
练习:一批物资要用11辆汽车从甲地运到360千米外的乙地,,若车速为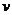 千米/小时,两车的距离不能小于
千米/小时,两车的距离不能小于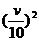 千米,运完这批物资至少需要
千米,运完这批物资至少需要 小时.
小时.
[课堂小结]
[课堂检测]
2.(1) 若正数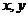 满足
满足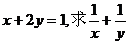 的最小值;
的最小值;
(2) 若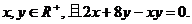 求
求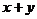 的最小值.
的最小值.
1.已知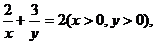 则
则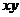 的最小值是
的最小值是 .
.
4.设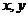 为正实数,且
为正实数,且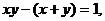 则
则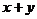 有最 值是
;
有最 值是
;
[典型例题讲练]
例1.已知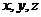 是实数,
是实数,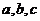 是正实数,
是正实数,
求证: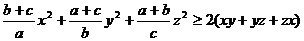
练习:①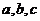 是不全相等的实数,求证:
是不全相等的实数,求证: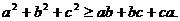
②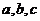 是实数,求证:
是实数,求证: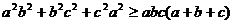
例2.⑴设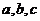 都是正数, 且
都是正数, 且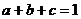 ,求证:
,求证: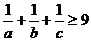 ;
;
⑵已知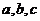 为不全相等的正数,
为不全相等的正数,
求证: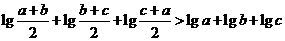 .
.
练习:
已知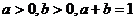 求证:
求证: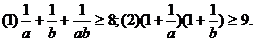
[课堂小结]
[课堂检测]
3.已知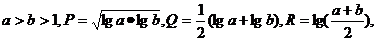 则
则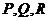 的大小关系是
的大小关系是 .
.
2. 已知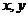 均为正数,且
均为正数,且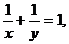 ,则
,则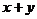 的最小值是
的最小值是
1.
函数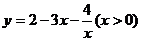 的最大值为
的最大值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com