
3.椭圆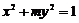 的焦点在
的焦点在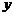 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则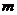 的值为____________.
的值为____________.
2.若焦点在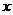 轴上的椭圆
轴上的椭圆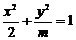 的离心率为
的离心率为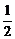 ,则
,则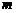 =______________.
=______________.
1.椭圆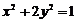 的离心率是______________,准线方程是______________________
的离心率是______________,准线方程是______________________
2. 平面内有两定点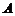 、
、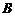 及动点
及动点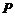 .命题
.命题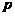 :
: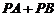 为定值,命题
为定值,命题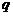 :点
:点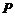 的轨迹是以
的轨迹是以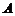 、
、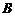 为焦点的椭圆,那么
为焦点的椭圆,那么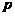 是
是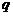 的( )
的( )
|
A.充分不必要条件 |
B.必要不充分条件 |
C.充要条件 |
D.既不充分也不必要条件 |
3设椭圆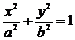
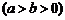 的焦点为
的焦点为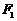 、
、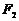 ,长轴两端点为
,长轴两端点为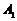 、
、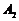 .(1)
.(1)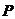 为椭圆上一点,且
为椭圆上一点,且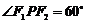 ,求
,求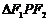 的面积;(2)若椭圆上存在一点
的面积;(2)若椭圆上存在一点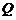 ,使
,使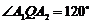 求椭圆离心率
求椭圆离心率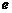 的取值范围.
的取值范围.
§78 椭圆(2)
例3 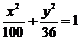 上一点
上一点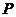 到右准线的距离为10,那么
到右准线的距离为10,那么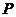 点到它的左焦点的距离是_____.
点到它的左焦点的距离是_____.
练习 点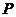 在椭圆
在椭圆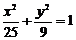 上,它到左焦点的距离是它到右焦点距离的两倍,则点
上,它到左焦点的距离是它到右焦点距离的两倍,则点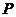 的横坐标是____________.
的横坐标是____________.
例2 若椭圆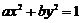 与直线
与直线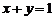 交于
交于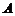 、
、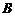 两点,
两点,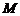 为
为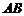 的中点,直线
的中点,直线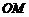 (
(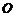 为原点)的斜率为
为原点)的斜率为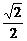 ,(1)求
,(1)求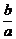 ;(2)若
;(2)若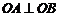 ,求椭圆的方程.
,求椭圆的方程.
变式 直线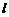 过点
过点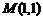 ,与椭圆
,与椭圆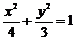 相交于
相交于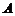 、
、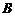 两点,若
两点,若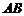 的中点为
的中点为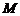 ,试求直线
,试求直线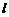 的方程.
的方程.
[课堂小结]
[课堂检测]
4. 椭圆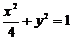 的焦点为
的焦点为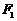 、
、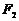 ,点
,点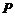 为椭圆上一动点,当
为椭圆上一动点,当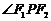 为钝角时,则点
为钝角时,则点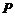 的横坐标
的横坐标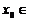 __________________.
__________________.
[典型例题]
例1 求满足下列条件的椭圆的标准方程:
(1) 与椭圆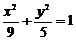 有相同焦点且过点
有相同焦点且过点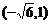
(2) 与椭圆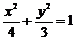 有相同离心率且过点
有相同离心率且过点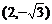 .;
.;
练习 已知三点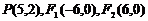 .(1)求以
.(1)求以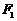 、
、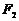 为焦点且过点的椭圆的标准方程;
为焦点且过点的椭圆的标准方程;
(2)设点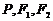 关于直线
关于直线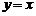 的对称点分别为
的对称点分别为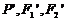 ,求以
,求以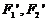 为焦点且过点
为焦点且过点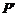 的双曲线的标准方程.
的双曲线的标准方程.
例1
一动圆与已知圆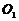 :
: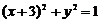 外切,与圆
外切,与圆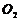 :
: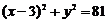 内切,试求动圆圆心的轨迹方程.
内切,试求动圆圆心的轨迹方程.
练习 已知动圆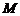 过定点
过定点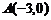 ,并且在定圆
,并且在定圆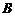 :
: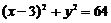 的内部与其相内切,求动圆圆心的轨迹方程.
的内部与其相内切,求动圆圆心的轨迹方程.
[课堂小结]
[课堂检测]
1求满足下列条件的椭圆的标准方程:
(1) 短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为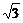
(2) 经过点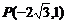 ,
,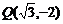 .
.
3. 如果方程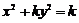 表示焦点在
表示焦点在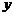 轴上的椭圆,则实数
轴上的椭圆,则实数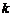 的取值范围是_____________
的取值范围是_____________
2. 若椭圆的长轴是短轴的3倍,且经过点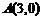 ,则椭圆标准方程为___________________.
,则椭圆标准方程为___________________.
1. 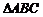 中,若
中,若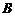 、
、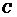 的坐标分别为
的坐标分别为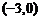 、
、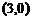 ,且
,且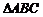 的周长等于16,则顶点
的周长等于16,则顶点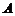 的轨迹方程为___________________.
的轨迹方程为___________________.
2. 已知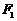 、
、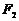 是椭圆
是椭圆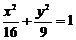 的两个焦点,过
的两个焦点,过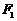 的直线与椭圆交于
的直线与椭圆交于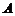 、
、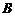 两点,则
两点,则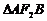 的周长为______________.
的周长为______________.
[基本训练]
1. 椭圆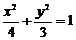 的长轴位于_____轴,长轴长等于_____;短轴位于_____轴,短轴长等于_____;焦点在_____轴上,焦点坐标分别是________和________;离心率
的长轴位于_____轴,长轴长等于_____;短轴位于_____轴,短轴长等于_____;焦点在_____轴上,焦点坐标分别是________和________;离心率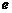 =_____;左顶点坐标是________;下顶点坐标是________;椭圆上点
=_____;左顶点坐标是________;下顶点坐标是________;椭圆上点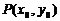 的横坐标的范围是___________,纵坐标的范围是___________;
的横坐标的范围是___________,纵坐标的范围是___________;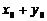 的取值范围是______________.
的取值范围是______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com