
4.试用向量证明三垂线定理及其逆定理.
已知:如下图,PO、PA分别是平面α的垂线和斜线,OA是PA在α内的射影,a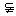 α,求证:a⊥PA
α,求证:a⊥PA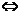 a⊥OA.
a⊥OA.
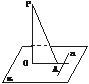
证明:设直线a上非零向量a,要证a⊥PA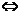 a⊥OA,即证a·
a⊥OA,即证a·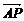 =0
=0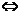 a·
a·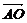 =0.
=0.
∵a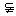 α,a·
α,a·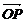 =0,∴a·
=0,∴a·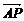 =a·(
=a·(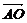 +
+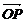 )=a·
)=a·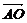 +a·
+a·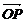 =a·
=a·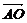 .
.
∴a·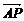 =0
=0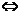 a·
a·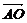 =0,即a⊥PA
=0,即a⊥PA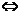 a⊥OA.
a⊥OA.
评述:向量的数量积为零是证明空间直线垂直的重要工具.在应用过程中,常需要通过加、减法对向量进行转换,当然,转换的方向是有利于计算向量的数量积.
3.已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则〈a,b〉=_____________.
解析:由条件知(a+3b)·(7a-5b)=7|a|2-15|b|2+16a·b=0,及(a-4b)·(7a-2b)=
7|a|2+8|b|2-30a·b=0.两式相减得46a·b=23|b|2,∴a·b=  |b|2.代入上面两个式子中的任意一个,即可得到|a|=|b|.∴cos〈a,b〉=
|b|2.代入上面两个式子中的任意一个,即可得到|a|=|b|.∴cos〈a,b〉=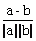 =
=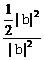 =
= .
.
∴〈a,b〉=60°.
答案:60°
2.O、A、B、C为空间四个点,又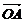 、
、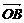 、
、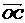 为空间的一个基底,则
为空间的一个基底,则
A.O、A、B、C四点不共线 B.O、A、B、C四点共面,但不共线
C.O、A、B、C四点中任意三点不共线 D.O、A、B、C四点不共面
解析:由基底意义,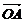 、
、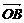 、
、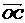 三个向量不共面,但A、B、C三种情形都有可能使
三个向量不共面,但A、B、C三种情形都有可能使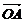 、
、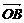 、
、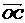 共面.只有D才能使这三个向量不共面,故应选D.
共面.只有D才能使这三个向量不共面,故应选D.
答案:D
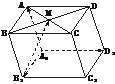
1.平行六面体ABCD-A1B1C1D1中,M为AC和BD的交点,若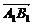 =a,
=a,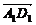 =b,
=b,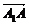 =
=
c,则下列式子中与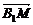 相等的是
相等的是
A.-
 a+
a+  b+c B.
b+c B.
 a+
a+  b+c
b+c
C.  a-
a-  b+c D.-
b+c D.-
 a-
a-  b+c
b+c
解析: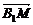 =
=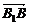 +
+ 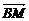 =
=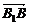 +
+  (
(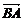 +
+ )=
)=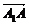 -
- 
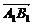 +
+ 
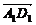 =c-
=c-  a+
a+  b,故选A.
b,故选A.
答案:A
5.已知四边形ABCD中,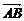 =a-2c,
=a-2c, =5a+6b-8c,对角线AC、BD的中点分别为E、F,则
=5a+6b-8c,对角线AC、BD的中点分别为E、F,则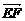 =_____________.
=_____________.
解析:∵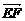 =
=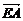 +
+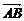 +
+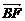 ,
,
又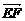 =
=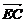 +
+ +
+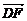 ,
,
两式相加,得2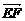 =(
=(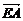 +
+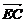 )+(
)+(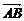 +
+ )+(
)+(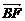 +
+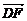 ).
).
∵E是AC的中点,
故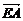 +
+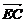 =0.同理,
=0.同理,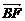 +
+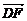 =0.
=0.
∴2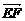 =
= 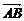 +
+ =(a-2c)+(5a+6b-8c)=6a+6b-10c.∴
=(a-2c)+(5a+6b-8c)=6a+6b-10c.∴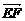 =3a+3b-5c.
=3a+3b-5c.
答案:3a+3b-5c
●典例剖析
[例1] 证明空间任意无三点共线的四点A、B、C、D共面的充分必要条件是:对于空间任一点O,存在实数x、y、z且x+y+z=1,使得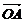 =x
=x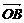 +y
+y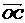 +z
+z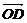 .
.
剖析:要寻求四点A、B、C、D共面的充要条件,自然想到共面向量定理.
解:依题意知,B、C、D三点不共线,则由共面向量定理的推论知:四点A、B、C、D共面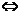 对空间任一点O,存在实数x1、y1,使得
对空间任一点O,存在实数x1、y1,使得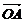 =
=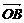 +x1
+x1 +y1
+y1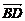 =
=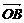 +x1(
+x1(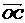 -
-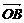 )+y1(
)+y1(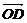 -
-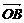 )=(1-x1-y1)
)=(1-x1-y1)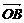 +x1
+x1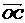 +y1
+y1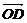 ,取x=1-x1-y1、y=x1、z=y1,则有
,取x=1-x1-y1、y=x1、z=y1,则有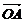 =x
=x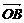 +y
+y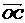 +z
+z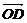 ,且x+y+z=1.
,且x+y+z=1.
特别提示
向量基本定理揭示了向量间的线性关系,即任一向量都可由基向量唯一的线性表示,为向量的坐标表示奠定了基础.共(线)面向量基本定理给出了向量共(线)面的充要条件,可用以证明点共(线)面.本题的结论,可作为证明空间四点共面的定理使用.
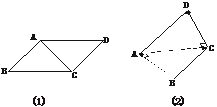
[例2] 在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B、D间的距离.
解:如下图,因为∠ACD=90°,
所以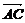 ·
· =0.同理,
=0.同理,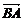 ·
·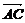 =0.
=0.
因为AB与CD成60°角,
所以〈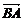 ,
, 〉=60°或120°.因为
〉=60°或120°.因为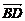 =
=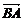 +
+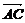 +
+ ,
,
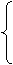 所以
所以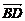 2=
2=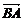 2+
2+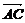 2+
2+ 2+2
2+2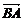 ·
·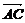 +2
+2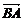 ·
· +2
+2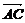 ·
· =
=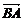 2+
2+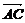 2+
2+ 2+2
2+2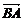 ·
· =3+2×1×1×cos〈
=3+2×1×1×cos〈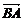 ,
, 〉= 4
(〈
〉= 4
(〈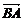 ,
, 〉=60°),
〉=60°),
2
(〈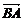 ,
, 〉=120°).
〉=120°).
所以|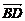 |=2或
|=2或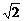 ,
,
即B、D间的距离为2或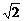 .
.
[例3] 在棱长为1的正方体ABCD-A1B1C1D1中,BD1交平面ACB1于点E,
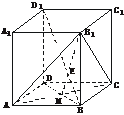
求证:(1)BD1⊥平面ACB1;
(2)BE= ED1.
ED1.
证明:(1)我们先证明BD1⊥AC.
∵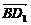 =
=  +
+  +
+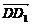 ,
,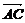 =
= 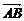 +
+ ,
,
∴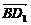 ·
·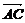 =(
=( +
+ +
+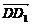 )·(
)·(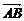 +
+ )=
)= ·
· +
+
 ·
·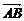 =
= ·
· -
-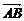 ·
·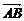 =|
=| |2-|
|2-|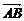 |2=1-1=0.
|2=1-1=0.
∴BD1⊥AC.同理可证BD1⊥AB1,于是BD1⊥平面ACB1.
(2)设底面正方形的对角线AC、BD交于点M,则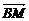 =
= 
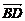 =
= 
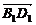 ,即2
,即2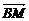 =
=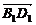 .对于空间任意一点O,设
.对于空间任意一点O,设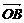 =b,
=b,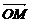 =m,
=m,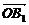 =b1,
=b1,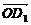 =d1,则上述等式可改写成2(m-b)=d1-b1或b1+2m=d1+2b.记
=d1,则上述等式可改写成2(m-b)=d1-b1或b1+2m=d1+2b.记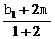 =
=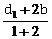 =e.此即表明,由e向量所对应的点E分线段B1M及D1B各成λ(λ=2)之比,所以点E既在线段B1M(B1M
=e.此即表明,由e向量所对应的点E分线段B1M及D1B各成λ(λ=2)之比,所以点E既在线段B1M(B1M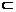 面ACB1)上又在线段D1B上,所以点E是D1B与平面ACB1之交点,此交点E将D1B分成2与1之比,即D1E∶EB=2∶1.∴BE=
面ACB1)上又在线段D1B上,所以点E是D1B与平面ACB1之交点,此交点E将D1B分成2与1之比,即D1E∶EB=2∶1.∴BE= ED1.
ED1.
思考讨论
利用空间向量可以解决立体几何中的线线垂直、线线平行、四点共面、求长度、求夹角等问题.
●闯关训练
夯实基础
4.已知a=(1,0),b=(m,m)(m>0),则〈a,b〉=_____________.
答案:45°
3.在平行六面体ABCD-A′B′C′D′中,向量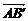 、
、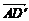 、
、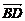 是
是
A.有相同起点的向量 B.等长的向量
C.共面向量 D.不共面向量
解析:∵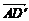 -
-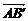 =
=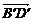 =
=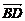 ,
,
∴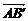 、
、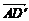 、
、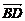 共面.
共面.
答案:C
2.设向量a、b、c不共面,则下列集合可作为空间的一个基底的是
A.{a+b,b-a,a} B.{a+b,b-a,b}
C.{a+b,b-a,c} D.{a+b+c,a+b,c}
解析:由已知及向量共面定理,易得a+b,b-a,c不共面,故可作为空间的一个基底,故选C.
答案:C
1.在以下四个式子中正确的有
a+b·c,a·(b·c),a(b·c),|a·b|=|a||b|
A.1个 B.2个 C.3个 D.0个
解析:根据数量积的定义,b·c是一个实数,a+b·c无意义.实数与向量无数量积,故a·(b·c)错,|a·b|=|a||b||cos〈a,b〉|,只有a(b·c)正确.
答案:A
9.6 空间向量及其运算(B)
●知识梳理
空间两个向量的加法、减法法则类同于平面向量,即平行四边形法则及三角形法则.
a·b=|a||b|cos〈a,b〉.
a2=|a|2.
a与b不共线,那么向量p与a、b共面的充要条件是存在实数x、y,使p=xa+yb.
a、b、c不共面,空间的任一向量p,存在实数x、y、z,使p=xa+yb+zc.
●点击双基
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com