19．(1)证明：因为E、F分别为△DCP中CD、PD边的中点，所以PC//EF.

　　　　 又PC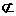平面FAE，EF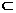平面FAE，所以PC//平面FAE.

　　　　 AD=AC. 在ACD中，由E是CD中点，

　 　　　∴有CD⊥AE.

　　　　　　　 设H、M分别为AE、AD的中点，连结FM、MH.

　　　　 因为点F是PD的中点，所以FM//PA，MH//DE.

　　　　 由PA⊥平面ABCD，知FM⊥平面ABCD.

　　　　 由CD⊥AE，知：MH⊥AE.

　　　　　　　 连结FH，则FH⊥AE，所以∠FHM即为所求二面角的平面角.

　　　　 设PA=AD=1，则

　　　　 在Rt△FMH中，

　　　　 所以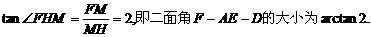

　 (3)解：当.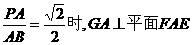

　　　　 由(2)可知：CD⊥AE，又AB//CD，所以AB⊥AE.

　　　　 由PA⊥平面ABCD，知PA⊥AE.

　　　　 又PA∩AB=A，所以AE⊥平面PAB. 又GA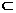平面PAB，所以GA⊥AE.

　　　　 所以，要使GA⊥平面FAE，只需GA⊥AF.

在Rt△PAB中，设PA=x，AB=AD=y. 则AG=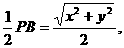

同理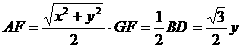

在△GAF中，令AG²+AF²=GF²，解得.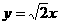

所以，当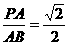时，GA⊥平面FAE.　　　　　　　　　　　　　

19．(本小题满分12分) 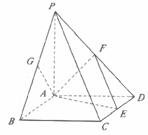　 如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA⊥平面ABCD，点E、F、G分别为CD、PD、PB的中点.

　 (1)证明PC//平面FAE；

　 (2)若PA=AD，求二面角F-AE-D的大小；

　 (3)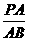为何值时，GA⊥平面FAE？证明你的结论.

18．解：(1)设一天同为黑色鱼的概率为P₁，同为红色鱼的概率为P₂，

则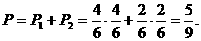

答：这位生物老师在一天中上、下午所捞的鱼为同色的概率为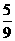

(2)有两个不同色的概率为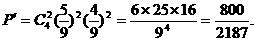

答：这位生物老师一周中恰有两天上、下午所捞得的鱼为不同色的概率为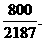

18．(本小题满分12分)

　　　　 某学校的生物实验室里有一个鱼缸，里面有6条鱼，其中4条黑色的和2条红色的，有位生物老师每周4天有课，每天上、下午各一节课，每节课前从鱼缸中任意捞取1条鱼在课上用，用后再放回鱼缸.

　 (1)求这位生物老师在一天中上、下午所捞的鱼为同色的概率；

　 (2)求这位生物老师一周中恰有两天上、下午所捞得的鱼为不同色的概率.

17．解：(1)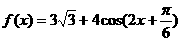

，

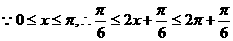
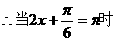　 (2)由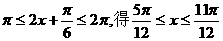　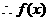 的单调增区间的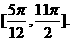

17．(本小题满分12分)已知函数.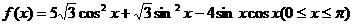

　 (1)求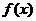的最小值；

　 (2)求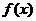的单调递增区间.

16．下面有4个命题：

　　 ①若a、b为一平面内两非零向量，则a⊥b是|a+b|=|a－b|的充要条件；

　　　 ②一平面内的两条曲线的方程分别是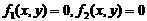，它们的交点是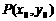，则方程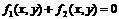的曲线经过点P；

　　　 ③经过一点且和一条已知直线垂直的所有直线都在同一平面内；

　　　 ④已知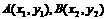是抛物线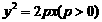上不同的两个点，则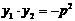是直线AB通过抛物线焦点的必要不充分条件.

　　 其中真命题的序号是　　　　 ①②③　　　 (把符合要求的命题序号都填上)

15．如果三位数的十位数字大于百位数字，也大于个位数字，则这样的三位数一共有　　　

　　 　　　240　　　　　　 .(作数字作答)

14．圆心在(2，－3)点，且被直线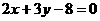截得的弦长为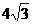的圆的标准方程为

　　 　　　　　　　　　.

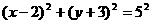13．若在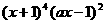的展开式中x的系数是6，则a=　　　 －1　　　　 .