
题目列表(包括答案和解析)
4.已知直线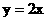 上一点P的横坐标为a,有两个点A(-1,1),B(3,3),那么使向量
上一点P的横坐标为a,有两个点A(-1,1),B(3,3),那么使向量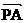 与
与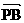 夹角为钝角的一个充分但不必要的条件是
( B )
夹角为钝角的一个充分但不必要的条件是
( B )
A.-1<a<2 B.0<a<1 C.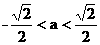 D.0<a<2
D.0<a<2
3.在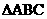 中,已知sinC=2sin(B+C)cosB,那么
中,已知sinC=2sin(B+C)cosB,那么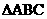 一定是
( B )
一定是
( B )
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.等边三角形
2.已知(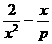 )
)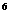 的展开式中,不含x的项是
的展开式中,不含x的项是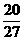 ,那么正数p的值是
( C )
,那么正数p的值是
( C )
A. 1 B.2 C.3 D.4
1.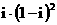 等于
( D
)
等于
( D
)
A.2-2i B.2+2i C.-2 D.2
22.(本题满分18分,其中第(1)小题6分,第(2)小题6分,第(3)小题6分)
如图所示,是树形图形.第一层是一条与水平线垂直的线段,长度为1;第二层在第一层线段的前端作两条与该段均成1350的线段,长度为其一半;第三层按第二层的方法在每一线段的前端生成两条线段;重复前面的作法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度。
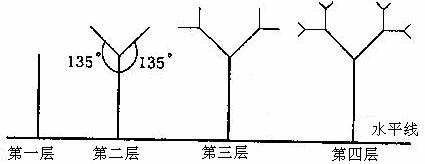
1)求第三层及第四层树形图的高度H3,H4;
2)求第n层树形图的高度Hn;
3)若树形图的高度大于2,则称树形图为“高大”,否则称为“矮小”。显然,当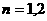 时是“矮小”的,是否存在
时是“矮小”的,是否存在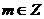 。使得当
。使得当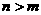 时,该树形图是“高大”的?
时,该树形图是“高大”的?
21.(本题满分16分,其中第(1)小题8分,第(2)小题8分)
已知存在实数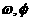 (其中
(其中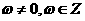 )使得函数
)使得函数 是奇函数,且在
是奇函数,且在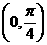 上是增函数。
上是增函数。
(1)试用观察法猜出两组 与
与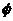 的值,并验证其符合题意;
的值,并验证其符合题意;
(2)求出所有符合题意的 与
与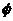 的值。
的值。
20.(本题满分14分,第(1)小题6分,(2)小题8分)
在平面直角坐标系中,若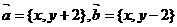 ,且
,且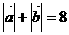 。
。
(1)求动点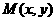 的轨迹C的方程;
的轨迹C的方程;
(2)过点(0,3)作直线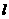 与曲线C交于A、B两点,设
与曲线C交于A、B两点,设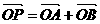 ,是否存在这样的直线
,是否存在这样的直线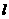 ,使得四边形OAPB为矩形?若存在,求出直线
,使得四边形OAPB为矩形?若存在,求出直线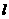 的方程,不存在,说明理由。
的方程,不存在,说明理由。
19.(本题满分14分,第(1)小题6分,(2)小题8分)
设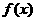 是
是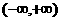 上的奇函数,对任意实数x,都有
上的奇函数,对任意实数x,都有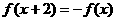 ,当
,当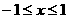 时,
时,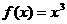 。
。
(1) 试证: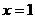 是函数
是函数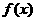 的一条对称轴;
的一条对称轴;
(2) 证明函数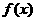 是以4为周期的函数,并求
是以4为周期的函数,并求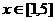 时,
时,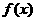 的解析式。
的解析式。
18.(本题满分12分,第(1)6分,第(2)6分)
某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如ΔDQH等)上铺草坪,造价为80元/m2。
(1) 设总造价为S元,AD长为xm,试建立S与x的函数关系;
(2) 当x为何值时,S最小?并求这个最小值。
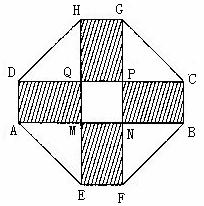
第18题图
17.(本题满分12分)已知x∈R,z∈C,x、z满足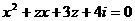 。
。
(1) 若z在复平面内对应的点Z在第一象限,求x的范围;
(2)
是否存在这样x,使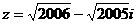 成立。
成立。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com