
题目列表(包括答案和解析)
3、直线是平面几何的基本图形,它与方程中的二元一次方程Ax+By+C=0(A2+B2≠0)一一对应。
从几何条件看,已知直线上一点及直线方向与已知直线上两点均可确定直线;从对应方程看,直线方程两种典型形式:点斜式(斜截式),两点式(截距式),因此求直线方程,常用待定系数法。即根据题意,选择方程的适当形式;由已知条件,列关于参数的方程(组)。
当点P(x0,y0)在直线Ax+By+C=0上时,其坐标满足方程Ax0+By0+C=0;当P不在直线Ax+By+C=0上时,Ax0+By0+C≠0,即Ax0+By0+C>0或Ax0+By0+C<0。这就是二元一次不等式的几何意义:二元一次不等式Ax+By+C>0(或<0)表示直线Ax+By+C=0上方或下方区域,其具体位置的确定常用原点(0,0)代入检验。利用此几何意义,可以解决一类二元函数的最值问题。这就是线性规划的内容。
因直线与二元一次方程Ax+By+C=0(A2+B2≠0)一一对应,即由有序数组(A,B,C)确定,因此研究直线与直线之间的位置关系就是考察直线对应的数组间关系。
设直线1:A1x+B1y+C1=0(A12+B12≠0),直线2:A2x+B2y+C2=0(A22+B22≠0)
则:1∥2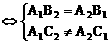
1与2相交 A1B2≠A2B1
A1B2≠A2B1
其夹角公式为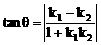 ,其中k1,k2分别表示1及2斜率,当1或2斜率不存在时,画图通过三角形求解,1与2夹角为θ∈(0,
,其中k1,k2分别表示1及2斜率,当1或2斜率不存在时,画图通过三角形求解,1与2夹角为θ∈(0,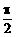 ]
]
特例:1⊥2 A1A2+B1B2=0(此时不能用夹角公式求解)
A1A2+B1B2=0(此时不能用夹角公式求解)
利用点P(x0,y0)到直线:Ax+By+C=0的距离公式d=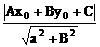 可以求出两平行直线:Ax+By+C1=0,Ax+By+C2=0(C1≠C2)间的距离d=
可以求出两平行直线:Ax+By+C1=0,Ax+By+C2=0(C1≠C2)间的距离d=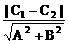 。
。
2、直线的倾斜角α和斜率k是描述直线位置的重要参数,它们之间关系是正切函数关系:k=tanα,α∈[0,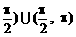 ,当α=
,当α=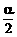 时,直线斜率不存在,否则由α求出唯一的k与之对应。
时,直线斜率不存在,否则由α求出唯一的k与之对应。
当已知k,求倾斜角α时:k≥0时,α=arctank;k<0时,α=π+arctank。或:k=0时,α=0;k≠0时,cotα=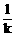 ,α=arccot
,α=arccot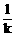 。
。
由正切函数可知,当α∈(0,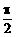 ),α递增时,斜率k→+∞。当α∈(
),α递增时,斜率k→+∞。当α∈(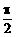 ,π),α递减时,斜率k→-∞。
,π),α递减时,斜率k→-∞。
当涉及到斜率参数时,通常对k是否存在分类讨论。
1、曲线和方程是中学数学的两种常见研究对象。借助于平面直角坐标系,形和数可
以得到高度的统一,它们最基本的对应关系是点和有序数对的一一对应。当点运动形成轨迹时,对应坐标便会满足一个方程。当曲线C和方程F(x,y)=0满足如下关系时:①曲线C上点的坐标都是方程F(x,y)=0的解;②以方程F(x,y)=0的解为坐标的点都在曲线C上,则称曲线C为方程F(x,y)=0表示的曲线;方程F(x,y)=0是曲线C表示的方程。从集合角度看,点集(曲线)与方程解集相等。解析几何研究的内容就是给定曲线C,如何求出它所对应的方程,并根据方程的理论研究曲线的几何性质。其特征是以数解形。坐标法是几何问题代数化的重要方法。
3、直线和圆位置关系的研究。
2、圆的方程三种形式,如何求圆的方程。
1、直线方程的五种表现形式,如何求直线方程;二元一次不等式的几何意义及运用。
(三)解答题
16、已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,求这个数列的公比和项数。
17、已知等比数列{an}的首项为a1>0,公比q>-1(q≠1),设数列{bn}的通项bn=an+1+an+2(n∈N+),数列{an},{bn}的前n项和分别记为An,Bn,试比较An与Bn大小。
18、数列{an}中,a1=8,a4=2且满足an+2=2an+1-an(n∈N+)
(1)求数列{an}通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn;
(3)设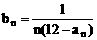 (n∈N+)Tn=b1+b2+…+bn,是否存在最大的整数m,使得对于任意的n∈N+,均有
(n∈N+)Tn=b1+b2+…+bn,是否存在最大的整数m,使得对于任意的n∈N+,均有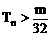 成立?若存在,求出m的值;若不存在,说明理由。
成立?若存在,求出m的值;若不存在,说明理由。
(二) 填空题
11、已知数列{an}满足a1+2a2+3a3+…+nan=n(n+1)(n+2),则它的前n项和Sn=______。
12、设等差数列{an}共有3n项,它的前2n项之和为100,后2n项之和为200,则该等差数列的中间n项的和等于
________。
13、设数列{an},{bn}(bn>0),n∈N+满足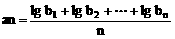 (n∈N+),则{an}为等差数列是{bn}为等比数
(n∈N+),则{an}为等差数列是{bn}为等比数
列的________条件。
14、长方体的三条棱成等比数列,若体积为216cm3,则全面积的最小值是______cm2。
15、若不等于1的三个正数a,b,c成等比数列,则(2-logba)(1+logca)=________。
(一) 选择题
1、已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<logmab<1,则m取值范围是
A、m>1 B、1<m<8 C、m>8 D、0<m<1或m>8
2、设a>0,b>0,a,x1,x2,b成等差数列,a,y1,y2,b成等比数列,则x1+x2与y1+y2的大小关系是
A、x1+x2≤y1+y2 B、x1+x2≥y1+y2 C、x1+x2<y1+y2 D、x1+x2>y1+y2
3、已知Sn是{an}的前n项和,Sn=Pn(P∈R,n∈N+),那么数列{an}
A、 是等比数列 B、当P≠0时是等比数列
C、 当P≠0,P≠1时是等比数列 D、不是等比数列
4、{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,则a3+a5等于
A、5 B、10 C、15 D、20
5、已知a,b,c成等差数列,则二次函数y=ax2+2bx+c的图象与x轴交点个数是
A、 0 B、1 C、2 D、1或2
6、设m∈N+,log2m的整数部分用F(m)表示,则F(1)+F(2)+…+F(1024)的值是
A、 8204 B、8192 C、9218 D、8021
7、若x的方程x2-x+a=0和x2-x+b=0(a≠b)的四个根可组成首项为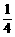 的等差数列,则a+b的值为
的等差数列,则a+b的值为
A、 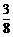 B、
B、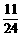 C、
C、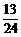 D、
D、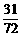
8、 在100以内所有能被3整除但不能被7整除的正整数和是
A、1557 B、1473 C、1470 D、1368
9、从材料工地运送电线杆到500m以外的公路,沿公路一侧每隔50m埋栽一根电线杆,已知每次最多只能运3根,要完成运载20根电线杆的任务,最佳方案是使运输车运行
A、 11700m B、14700m C、14500m D、14000m
10、已知等差数列{an}中,|a3|=|a9|,公差d<0,则使前n项和Sn取最大值的正整数n是
A、4或5 B、5或6 C、6或7 D、8或9
例1、已知数列{an}为等差数列,公差d≠0,其中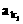 ,
,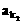 ,…,
,…,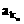 恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn。
恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn。
解题思路分析:
从寻找新、旧数列的关系着手
设{an}首项为a1,公差为d
∵ a1,a5,a17成等比数列
∴ a52=a1a17
∴(a1+4d)2=a1(a1+16d)
∴ a1=2d
设等比数列公比为q,则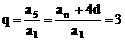
对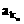 项来说,
项来说,
在等差数列中: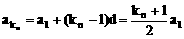
在等比数列中: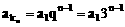
∴
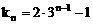
∴
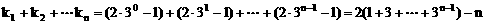
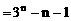
注:本题把k1+k2+…+kn看成是数列{kn}的求和问题,着重分析{kn}的通项公式。这是解决数列问题的一般方法,称为“通项分析法”。
例2、设数列{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,Tn为数列{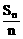 }的前n项和,求Tn。
}的前n项和,求Tn。
解题思路分析:
法一:利用基本元素分析法
设{an}首项为a1,公差为d,则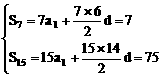
∴
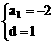
∴
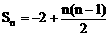
∴
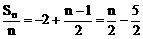
此式为n的一次函数
∴ {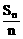 }为等差数列
}为等差数列
∴
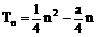
法二:{an}为等差数列,设Sn=An2+Bn
∴
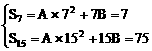
解之得: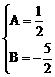
∴
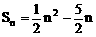 ,下略
,下略
注:法二利用了等差数列前n项和的性质
例3、正数数列{an}的前n项和为Sn,且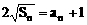 ,求:
,求:
(1)数列{an}的通项公式;
(2)设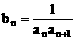 ,数列{bn}的前n项的和为Bn,求证:Bn
,数列{bn}的前n项的和为Bn,求证:Bn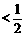 .
.
解题思路分析:
(I)涉及到an及Sn的递推关系,一般都用an=Sn-Sn-1(n≥2)消元化归。
∵
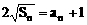
∴ 4Sn=(an+1)2
∴ 4Sn-1=(an-1+1)2(n≥2)
∴ 4(Sn-Sn-1)=(an+1)2-(an-1+1)2
∴ 4an=an2-an-12+2an-2an-1
整理得:(an-1+an)(an-an-1-2)=0
∵ an>0
∴ an-an-1=2
∴ {an}为公差为2的等差数列
在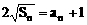 中,令n=1,a1=1
中,令n=1,a1=1
∴ an=2n-1
(II)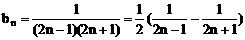
∴
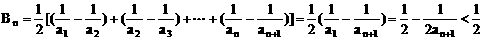
注:递推是学好数列的重要思想,例本题由4Sn=(an+1)2推出4Sn-1=(an-1+1)2,它其实就是函数中的变量代换法。在数列中一般用n-1,n+1等去代替n,实际上也就是说已知条件中的递推关系是关于n的恒等式,代换就是对n赋值。
例4、等差数列{an}中,前m项的和为77(m为奇数),其中偶数项的和为33,且a1-am=18,求这个数列的通项公式。
解题思路分析:
利用前奇数项和和与中项的关系
令m=2n-1,n∈N+
则
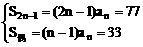
∴
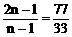
∴ n=4
∴ m=7
∴ an=11
∴ a1+am=2an=22
又a1-am=18
∴ a1=20,am=2
∴ d=-3
∴ an=-3n+23
例5、设{an}是等差数列,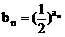 ,已知b1+b2+b3=
,已知b1+b2+b3=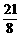 ,b1b2b3=
,b1b2b3=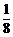 ,求等差数列的通项an。
,求等差数列的通项an。
解题思路分析:
∵ {an}为等差数列
∴ {bn}为等比数列
从求解{bn}着手
∵ b1b3=b22
∴
b23=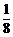
∴ b2=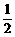
∴
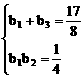
∴
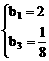 或
或 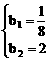
∴
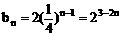 或
或 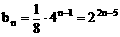
∵
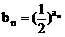
∴
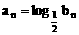
∴ an=2n-3 或 an=-2n+5
注:本题化归为{bn}求解,比较简单。若用{an}求解,则运算量较大。
例6、已知{an}是首项为2,公比为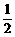 的等比数列,Sn为它的前n项和,
的等比数列,Sn为它的前n项和,
(1)用Sn表示Sn+1;
(2)是否存在自然数c和k,使得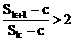 成立。
成立。
解题思路分析:
(1)∵ 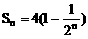
∴
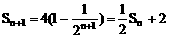
(2)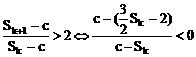 (*)
(*)
∵
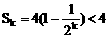
∴
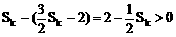
∴
式(*)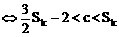 ①
①
∵ Sk+1>Sk
∴
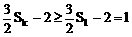
又Sk<4
∴ 由①得:c=2或c=3
当c=2时
∵ S1=2
∴ k=1时,c<Sk不成立,从而式①不成立
∵
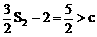
∴
由Sk<Sk+1得: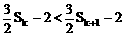
∴
当k≥2时,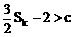 ,从而式①不成立
,从而式①不成立
当c=3时,S12,S2=3
∴ 当k=1,2时,C<Sk不成立
∴ 式①不成立
∵
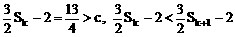
∴
当k≥3时,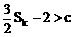 ,从而式①不成立
,从而式①不成立
综上所述,不存在自然数c,k,使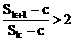 成立
成立
例7、某公司全年的利润为b元,其中一部分作为资金发给n位职工,资金分配方案如下:首先将职工按工作业绩(工作业绩均不相等)从大到小,由1到n排序,第1位职工得资金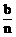 元,然后再将余额除以n发给第2位职工,按此方法将资金逐一发给每位职工,并将最后剩余部分作为公司发展基金。
元,然后再将余额除以n发给第2位职工,按此方法将资金逐一发给每位职工,并将最后剩余部分作为公司发展基金。
(1)设ak(1≤k≤n)为第k位职工所得资金额,试求a2,a3,并用k,n和b表示ak(不必证明);
(2)证明:ak<ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义。
解题思路分析:
谈懂题意,理清关系,建立模型
第1位职工的奖金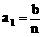
第2位职工的奖金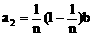
第3位职工的奖金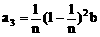
……
第k位职工的奖金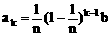
(2)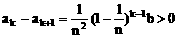
此奖金分配方案体现了“按劳分配”或“不吃大锅饭”等原则。
例8、试问数列{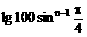 }的前多少项的和最大,并求这个最大值(lg2=0.3010)
}的前多少项的和最大,并求这个最大值(lg2=0.3010)
解题思路分析:
法一:
∴ {an}为首项为2,公差为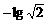 的等差数列
的等差数列
∴ 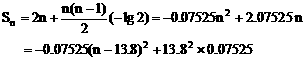
∵ n∈N+
∴ n=14时,(Sn)max=14.35
法二:∵ a1=2>0,d=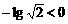
∴ {an}是递减数列,且Sn必为最大值
设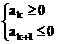
∴ 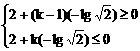
∴ 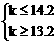
∴ k=14
∴ (Sn)max=S14=14.35
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com