
题目列表(包括答案和解析)
1、本章内容是初中《统计初步》与高中《概率》内容的深入和扩展,对数理统计中要研究的两个基本问题;如何从总体中抽取样本以及如何通过对所抽取的样本进行计算和分析,从而对总体的相应情况作出推断,作了初步的介绍。
几个基本名词:在统计中,考察对象的全体称为总体,总体中的每一个对象称为个体。
若记总体中N个个体取值分别为x1,x2,…,xN,则称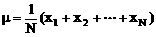 为总体平均数(μ为N个个体的算术平均数)
为总体平均数(μ为N个个体的算术平均数)
若记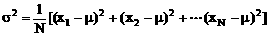 ,则称
,则称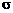 2为总体方差,
2为总体方差,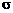 称为总体标准差。
称为总体标准差。
初中《统计初步》的主要内容
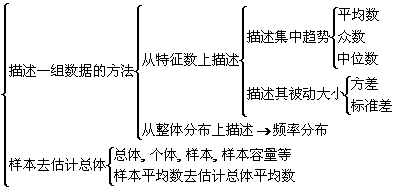
《统计》复习
(三)解答题
16、已知tan(α-β)=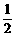 ,tanβ=
,tanβ=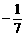 ,α,β∈(-π,0),求2α-β的值。
,α,β∈(-π,0),求2α-β的值。
17、是否存在实数a,使得函数y=sin2x+acosx+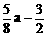 在闭区间[0,
在闭区间[0,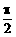 ]上的最大值是1?若存在,求出对应的a值。
]上的最大值是1?若存在,求出对应的a值。
18、已知f(x)=5sinxcosx-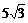 cos2x+
cos2x+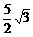 (x∈R)
(x∈R)
(1)求f(x)的最小正周期;
(2)求f(x)单调区间;
(二)填空题
11、函数f(x)=sin(x+θ)+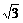 cos(x-θ)的图象关于y轴对称,则θ=________。
cos(x-θ)的图象关于y轴对称,则θ=________。
12、已知α+β=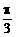 ,且
,且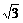 (tanαtanβ+c)+tanα=0(c为常数),那么tanβ=______。
(tanαtanβ+c)+tanα=0(c为常数),那么tanβ=______。
13、函数y=2sinxcosx-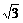 (cos2x-sin2x)的最大值与最小值的积为________。
(cos2x-sin2x)的最大值与最小值的积为________。
14、已知(x-1)2+(y-1)2=1,则x+y的最大值为________。
15、函数f(x)=sin3x图象的对称中心是________。
(一)选择题
1、下列函数中,既是(0,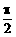 )上的增函数,又是以π为周期的偶函数是
)上的增函数,又是以π为周期的偶函数是
A、y=lgx2 B、y=|sinx| C、y=cosx
D、y=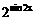
2、如果函数y=sin2x+acos2x图象关于直线x=-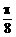 对称,则a值为
对称,则a值为
A、 -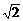 B、-1 C、1
D、
B、-1 C、1
D、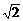
3、函数y=Asin(ωx+φ)(A>0,φ>0),在一个周期内,当x=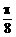 时,ymax=2;当x=
时,ymax=2;当x=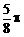 时,ymin=-2,则此函数解析式为
时,ymin=-2,则此函数解析式为
A、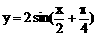 B、
B、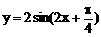 C、
C、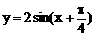 D、
D、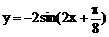
4、已知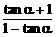 =1998,则
=1998,则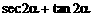 的值为
的值为
A、1997 B、1998 C、1999 D、2000
5、已知tanα,tanβ是方程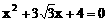 两根,且α,β
两根,且α,β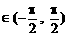 ,则α+β等于
,则α+β等于
A、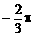 B、
B、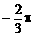 或
或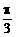 C、
C、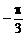 或
或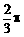 D、
D、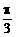
6、若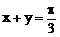 ,则sinx·siny的最小值为
,则sinx·siny的最小值为
A、-1
B、-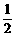 C、
C、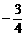 D、
D、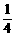
7、函数f(x)=3sin(x+100)+5sin(x+700)的最大值是
A、5.5 B、6.5 C、7 D、8
8、若θ∈(0,2π],则使sinθ<cosθ<cotθ<tanθ成立的θ取值范围是
A、(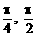 ) B、(
) B、(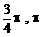 ) C、(
) C、(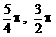 ) D、(
) D、(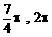 )
)
9、下列命题正确的是
A、若α,β是第一象限角,α>β,则sinα>sinβ
B、函数y=sinx·cotx的单调区间是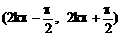 ,k∈Z
,k∈Z
C、函数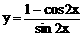 的最小正周期是2π
的最小正周期是2π
D、函数y=sinxcos2φ-cosxsin2x的图象关于y轴对称,则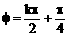 ,k∈Z
,k∈Z
10、函数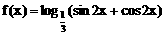 的单调减区间是
的单调减区间是
A、 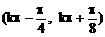 B、
B、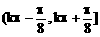 C.
C.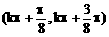 D、
D、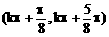 k∈Z
k∈Z
2、三角函数式asinx+bcosx是基本三角函数式之一,引进辅助角,将它化为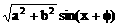 (取
(取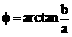 )是常用变形手段。特别是与特殊角有关的sin±cosx,±sinx±
)是常用变形手段。特别是与特殊角有关的sin±cosx,±sinx±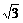 cosx,要熟练掌握变形结论。
cosx,要熟练掌握变形结论。
例3、 求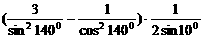 。
。
解题思路分析:
原式=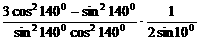
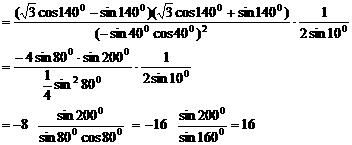
注:在化简三角函数式过程中,除利用三角变换公式,还需用到代数变形公式,如本题平方差公式。
例4、已知00<α<β<900,且sinα,sinβ是方程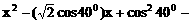
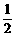 =0的两个实数根,求sin(β-5α)的值。
=0的两个实数根,求sin(β-5α)的值。
解题思路分析:
由韦达定理得sinα+sinβ=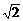 cos400,sinαsinβ=cos2400-
cos400,sinαsinβ=cos2400-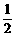
∴
sinβ-sinα=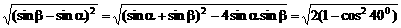
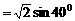
又sinα+sinβ=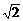 cos400
cos400
∴
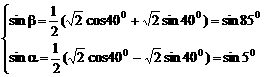
∵ 00<α<β< 900
∴
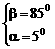
∴
sin(β-5α)=sin600=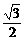
注:利用韦达定理变形寻找与sinα,sinβ相关的方程组,在求出sinα,sinβ后再利用单调性求α,β的值。
例5、(1)已知cos(2α+β)+5cosβ=0,求tan(α+β)·tanα的值;
(2)已知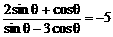 ,求
,求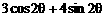 的值。
的值。
解题思路分析:
(1)从变换角的差异着手。
∵ 2α+β=(α+β)+α,β=(α+β)-α
∴ 8cos[(α+β)+α]+5cos[(α+β)-α]=0
展开得:
13cos(α+β)cosα-3sin(α+β)sinα=0
同除以cos(α+β)cosα得:tan(α+β)tanα=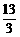
(2)以三角函数结构特点出发
∵
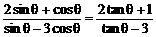
∴
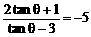
∴ tanθ=2
∴
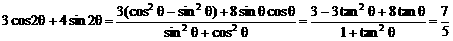
注;齐次式是三角函数式中的基本式,其处理方法是化切或降幂。
例6、已知函数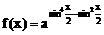 (a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
(a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
解题思路分析:
对三角函数式降幂
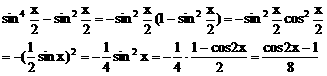
∴
f(x)=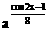
令
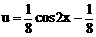
则 y=au
∴ 0<a<1
∴ y=au是减函数
∴
由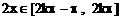 得
得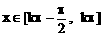 ,此为f(x)的减区间
,此为f(x)的减区间
由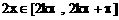 得
得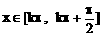 ,此为f(x)增区间
,此为f(x)增区间
∵ u(-x)=u(x)
∴ f(x)=f(-x)
∴ f(x)为偶函数
∵ u(x+π)=f(x)
∴ f(x+π)=f(x)
∴ f(x)为周期函数,最小正周期为π
当x=kπ(k∈Z)时,ymin=1
当x=kπ+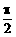 (k∈Z)时,ynax=
(k∈Z)时,ynax=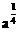
注:研究三角函数性质,一般降幂化为y=Asin(ωx+φ)等一名一次一项的形式。
例1、 已知函数f(x)=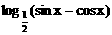
(1)求它的定义域和值域;
(2)求它的单调区间;
(3)判断它的奇偶性;
(4)判断它的周期性。
解题思路分析:
(1)x必须满足sinx-cosx>0,利用单位圆中的三角函数线及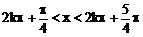 ,k∈Z
,k∈Z
∴
函数定义域为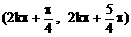 ,k∈Z
,k∈Z
 ∵
∵ 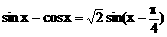
∴
当x∈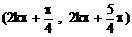 时,
时,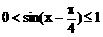
∴
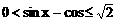
∴
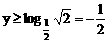
∴
函数值域为[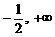 )
)
(3)∵ f(x)定义域在数轴上对应的点关于原点不对称
∴ f(x)不具备奇偶性
(4)∵ f(x+2π)=f(x)
∴ 函数f(x)最小正周期为2π
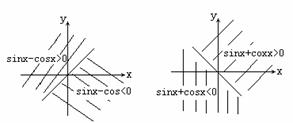
注;利用单位圆中的三角函数线可知,以Ⅰ、Ⅱ象限角平分线为标准,可区分sinx-cosx的符号;
以Ⅱ、Ⅲ象限角平分线为标准,可区分sinx+cosx的符号,如图。
例2、 化简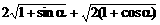 ,α∈(π,2π)
,α∈(π,2π)
解题思路分析:
凑根号下为完全平方式,化无理式为有理式
∵
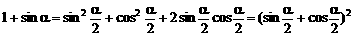
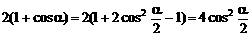
∴
原式=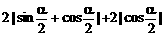
∵ α∈(π,2π)
∴
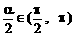
∴
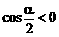
当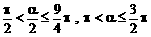 时,
时,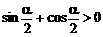
∴
原式=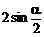
当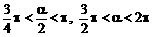 时,
时,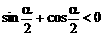
∴
原式=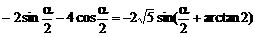
∴
原式=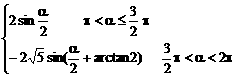
注:
1、本题利用了“1”的逆代技巧,即化1为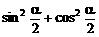 ,是欲擒故纵原则。一般地有
,是欲擒故纵原则。一般地有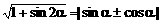 ,
,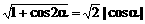 ,
,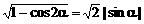 。
。
5、本章思想方法
(1)等价变换。熟练运用公式对问题进行转化,化归为熟悉的基本问题;
(2)数形结合。充分利用单位圆中的三角函数线及三角函数图象帮助解题;
(3)分类讨论。
4、三角函数的性质除了一般函数通性外,还出现了前面几种函数所没有的周期性。周期性的定义:设T为非零常数,若对f(x)定义域中的每一个x,均有f(x+T)=f(x),则称T为f(x)的周期。当T为f(x)周期时,kT(k∈Z,k≠0)也为f(x)周期。
三角函数图象是性质的重要组成部分。利用单位圆中的三角函数线作函数图象称为几何作图法,熟练掌握平移、伸缩、振幅等变换法则。
3、三角变换公式包括和、差、倍、半公式,诱导公式是和差公式的特例,对公式要熟练地正用、逆用、变用。如倍角公式:cos2α=2cos2α-1=1-2sin2α,变形后得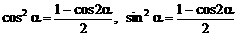 ,可以作为降幂公式使用。
,可以作为降幂公式使用。
三角变换公式除用来化简三角函数式外,还为研究三角函数图象及性质做准备。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com