
题目列表(包括答案和解析)
4.双曲线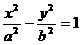 的左支上一点P,⊙O'为ΔPF1F2的内切圆,则圆心O'的横坐标为(
).
的左支上一点P,⊙O'为ΔPF1F2的内切圆,则圆心O'的横坐标为(
).
A、a
B、-a
C、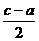 D、
D、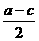
分析:设PF1,PF2,F1F2与内切圆⊙O'的切点分别为M,N,Q,由双曲线定义,
∵ |PF2|-|PF1|=2a, ∴ |PN|+|NF2|-(|PM|+|MF1|)=2a,
而 |DN|=|PM| ,|MF1|=|QF1|, |NF2|=|QF2| ∴ |QF2|-|QF1|=2a 又 |QF2|+|QF1|=2c,∴ |QF2|=a+c=c-xQ, ∴ xQ=-a, ∵O'Q⊥F1F2, ∴xQ'=xQ=-a, 选B.
3.F1、F2为椭圆两个焦点,Q为椭圆上任一点,以任一焦点作∠F1QF2的外角平分线的垂线,垂足为P,则P点轨迹为( ).
A、圆 B、椭圆 C、双曲线 D、抛物线
分析:延长F2P交F1Q的延长线为M,由椭圆定义及角平分线,
∵ 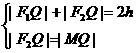 ∴
|F1Q|+|MQ|=|F1M|=2a,则点M(x0,y0)的轨迹方程为
∴
|F1Q|+|MQ|=|F1M|=2a,则点M(x0,y0)的轨迹方程为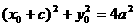 ......① 设P点坐标(x, y), ∵ P为F2M中点,
......① 设P点坐标(x, y), ∵ P为F2M中点,
∴ 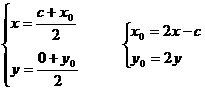 ,代入①,得 (2x-c+c)2+(2y)2=4a2,
∴ x2+y2=a2, 选A.
,代入①,得 (2x-c+c)2+(2y)2=4a2,
∴ x2+y2=a2, 选A.
2.设F1、F2为椭圆两焦点,点P是以F1,F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆离心率为( ).
A、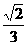 B、
B、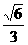 C、
C、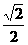 D、
D、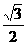
分析:P在以F1F2为直径的圆上,则∠F1PF2=90°,
而∠PF1F2=5PF2F1,∴
∠PF1F2=75°, ∠PF2F1=15°,∴ 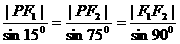 ,
,
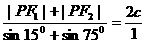 ,而|PF2|+|PF2|=2a,∴
,而|PF2|+|PF2|=2a,∴ 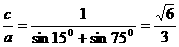 .
.
1.双曲线的虚轴长为4,离心率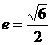 ,F1、F2分别是它的左,右焦点,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|为( ).
,F1、F2分别是它的左,右焦点,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|为( ).
A、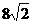 B、
B、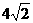 C、
C、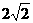 D、8
D、8
分析:利用双曲线定义, ∵ AB在左支上,∴|AF2|-|AF1|=2a, |BF2|-|BF1|=2a ∴ |AF2|+|BF2|-(|AF1|+|BF1|)=4a, 又∵ 2|AB|=|AF2|+|BF2|, |AF1|+|BF1|=|AB|
∴ 2|AB|-|AB|=4a. |AB|=4a,而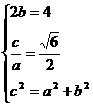 得
得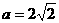 , ∴
, ∴ 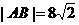 ,选A.
,选A.
7.若双曲线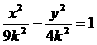 与圆x2+y2=1无公共点则k∈______.分析:同上题用数形结合的方法知
与圆x2+y2=1无公共点则k∈______.分析:同上题用数形结合的方法知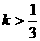 或
或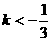 .
.
6.若椭圆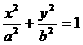 (a>b>0)与圆
(a>b>0)与圆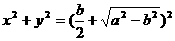 相交,则椭圆的离心率的取值范围为_______.
相交,则椭圆的离心率的取值范围为_______.
分析:圆锥曲线间的位置关系不能用联立方程,用判别式判定,一般来说应结合图形分析.
由图可知圆半径r满足 b<r<a,
∴ 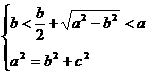 , 解得
, 解得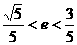 .
.
5.以3x-4y-2=0, 3x+4y-10=0为渐近线,以5y+4=0为一条准线的双曲线方程为_____.
分析:注意两条渐近线的交点,或一条渐近线和一条对称轴的交点都是双曲线的中心.
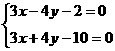 ,中心为(2,1),从而准线
,中心为(2,1),从而准线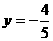 为下准线,焦点在平行于y轴的直线上,从而,中心与准线相矩
为下准线,焦点在平行于y轴的直线上,从而,中心与准线相矩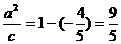 ……①,渐近线斜率为
……①,渐近线斜率为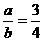 ……②
……②
联立①②,得a=3,
b=4, c=5.方程为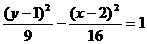 .
.
4.抛物线y2-2by+b2+4m-mx=0的准线与双曲线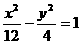 的右准线重合,则m的值为______.
的右准线重合,则m的值为______.
分析:首先将方程化为标准方程(y-b)2=m(x-4)
而双曲线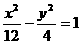 的右准线为x=3, 抛物线顶点(4,b)在x=3的右侧,
的右准线为x=3, 抛物线顶点(4,b)在x=3的右侧,
∴ 抛物线开口向右,m>0, 2p=m,∴ 焦准距(焦参数)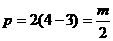 ,∴m=4.
,∴m=4.
3.若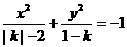 表示焦点在y轴上的双曲线,则它的半焦距的取值范围是( ).
表示焦点在y轴上的双曲线,则它的半焦距的取值范围是( ).
A、(1,+¥) B、(0,1) C、(1,2) D、与k有关
分析:首先应把方程标准化,方程可化为:
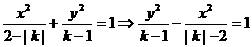
∴ 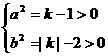 , ∴ k>2 c2=a2+b2=k-1+k-2=2k-3>2×2-3=1∴ c>1,选A.
, ∴ k>2 c2=a2+b2=k-1+k-2=2k-3>2×2-3=1∴ c>1,选A.
2.若双曲线的渐近线方程为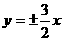 ,则其离心率为( ).
,则其离心率为( ).
A、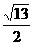 B、
B、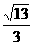 C、
C、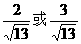 D、
D、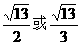
分析:当双曲线方程为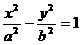 时,其渐近线为
时,其渐近线为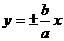 ,当双曲线方程为
,当双曲线方程为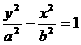 时,其渐近线为
时,其渐近线为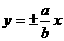 ,从而本题对应
,从而本题对应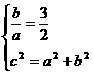 或
或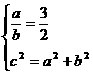 ,选D.
,选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com