
题目列表(包括答案和解析)
69、已知x>0,由不等式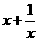 ≥2·
≥2·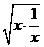 =2,
=2,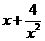 =
=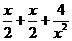 ≥
≥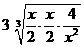 =3,
=3,
…,启发我们可以得出推广结论: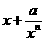 ≥n+1 (n∈N*),则a=_________
nn ______.
≥n+1 (n∈N*),则a=_________
nn ______.
68、已知函数y=f(x)满足f(a-tanθ)=cotθ-1,(其中,a、θ∈R均为常数)
(1)求函数y=f(x)的解析式;
(2)利用函数y=f(x)构造一个数列{xn},方法如下:
对于给定的定义域中的x1,令x2= f(x1),x3= f(x2),…,xn= f(xn-1),…
在上述构造过程中,如果xi(i=1,2,3,…)在定义域中,构造数列的过程继续下去;如果xi不在定义域中,则构造数列的过程停止.
① 如果可以用上述方法构造出一个常数列{xn},求a的取值范围;
② 如果取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求a实数的值.
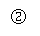
 解:(1)令
解:(1)令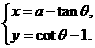 则
则 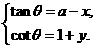
①×②,并整理,得 y=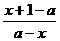 ,
,
∴y=f(x) =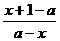 , (x≠a). ………………………………4分
, (x≠a). ………………………………4分
(2)①根据题意,只需当x≠a时,方程f(x) =x有解,
亦即方程 x2+(1-a)x+1-a=0 有不等于的解.
将x=a代入方程左边,得左边为1,故方程不可能有解x=a.
由 △=(1-a)2-4(1-a)≥0,得 a≤-3或a≥1,
即实数a的取值范围是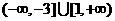 .
…………………………9分
.
…………………………9分
②根据题意,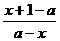 =a在R中无解,
=a在R中无解,
亦即当x≠a时,方程(1+a)x=a2+a-1无实数解.
由于x=a不是方程(1+a)x=a2+a-1的解,
所以对于任意x∈R,方程(1+a)x=a2+a-1无实数解,
∴ a= -1即为所求a的值. ……………………………………14分
67、定义:若存在常数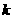 ,使得对定义域
,使得对定义域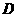 内的任意两个
内的任意两个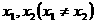 ,均有
,均有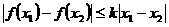 成立,则称函数
成立,则称函数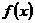 在定义域
在定义域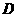 上满足利普希茨条件。若函数
上满足利普希茨条件。若函数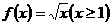 满足利普希茨条件,则常数
满足利普希茨条件,则常数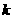 的最小值为
的最小值为 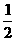 。
。
66、将侧棱相互垂直的三棱锥称为“直角三棱锥”,三棱锥的侧面和底面分别叫为直角三棱锥的“直角面和斜面”;过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”.请仿照直角三角形以下性质:
(1)斜边的中线长等于斜边边长的一半;
(2)两条直角边边长的平方和等于斜边边长的平方;
(3)斜边与两条直角边所成角的余弦平方和等于1.
写出直角三棱锥相应性质(至少一条): .
答案:(1) 斜面的中面面积等于斜面面积的四分之一;
(2)三个直角面面积的平方和等于斜面面积的平方;
(3)斜面与三个直角面所成二面角的余弦平方和等于1.
65、为了了解“预防禽流感疫苗”的使用情况,温州市卫生部门对本地区9月份至11月份使用疫苗的所有养鸡场进行了调查,根据下列图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为 90 万只.
 |
||||||||||
|
||||||||||
64、如图2,在正方体ABCD-A1B1C1D1中,M、N、P分别为棱AB、BC、DD1的中点.
(1)求二面角B1-MN-B的正切值;
(2)证明:PB⊥平面B1MN;
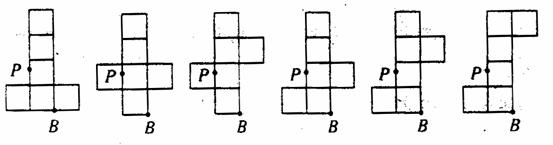
(3)画出该正方体表面展开图,使其满足“有4个正方形连成一个长方形”的条件.
符合条件的正方体表面展开图可以是以下6种情况之一.
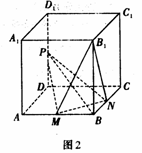
答案:
63、定义运算符号:“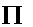 ”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作
”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作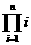 ,
,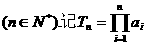 ,其中ai为数列
,其中ai为数列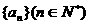 中的第i项.
中的第i项.
①若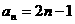 ,则T4=
;105;
,则T4=
;105;
②若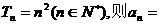 .
. 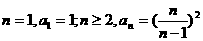
62、我们把平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为斜坐标系.平面上任意一点P的斜坐标定义为:若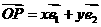 (其中
(其中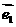 、
、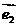 分别为斜坐标系的x轴、y轴正方向上的单位向量,x、y∈R),则点P的斜坐标为(x, y).在平面斜坐标系xoy中,若
分别为斜坐标系的x轴、y轴正方向上的单位向量,x、y∈R),则点P的斜坐标为(x, y).在平面斜坐标系xoy中,若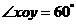 ,已知点M的斜坐标为 (1, 2),则点M到原点O的距离为
.
,已知点M的斜坐标为 (1, 2),则点M到原点O的距离为
. 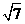
61、在4×□+9×□=60的两个□中,分别填入两自然数,使它们的倒数和最小,应分别填上 和 。
答案:设两数为x、y,即4x+9y=60,又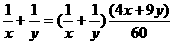 =
=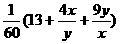 ≥
≥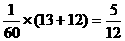 ,等于当且仅当
,等于当且仅当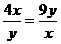 ,且4x+9y=60,即x=6且y=4时成立,故应分别有6、4。
,且4x+9y=60,即x=6且y=4时成立,故应分别有6、4。
60、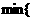
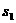 ,
,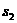 ,┅,
,┅,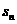
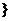 ,
,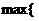
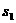 ,
,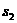 ,┅,
,┅,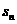
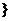 分别表示实数
分别表示实数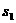 ,
,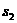 ,┅,
,┅,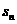 中的最小者和最大者.
中的最小者和最大者.
(1)作出函数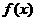 =|
=|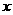 +3|+2|
+3|+2|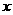 -1|(
-1|(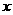 ∈R)的图像;
∈R)的图像;
(2)在求函数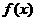 =|
=|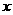 +3|+2|
+3|+2|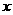 -1|(
-1|(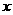 ∈R)的最小值时,有如下结论:
∈R)的最小值时,有如下结论:
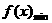 =
=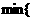
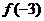 ,
,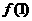
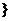 =4.请说明此结论成立的理由;
=4.请说明此结论成立的理由;
(3)仿照(2)中的结论,讨论当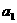 ,
,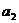 ,┅,
,┅,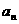 为实数时,
为实数时,
函数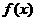 =
=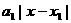 +
+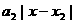 +┅+
+┅+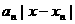
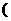
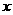 ∈R,
∈R,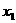 <
<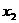 <┅<
<┅<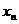 ∈R
∈R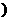 的最值.
的最值.
解:(1)图略;
(2)当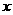 ∈(-∞,-3)时,
∈(-∞,-3)时,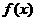 是减函数,
是减函数,
当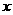 ∈
∈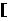 -3,1)时,
-3,1)时,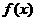 是减函数,
是减函数,
当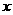 ∈
∈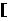 1,+∞)时,
1,+∞)时,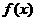 是增函数,
是增函数,
∴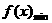 =
=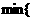
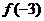 ,
,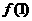
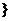 =4.
=4.
(3)当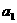 +
+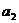 +┅+
+┅+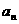 <0时,
<0时,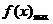 =
=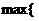
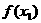 ,
,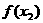 ,┅,
,┅,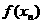
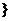 ;
;
当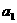 +
+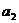 +┅+
+┅+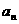 >0时,
>0时,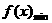 =
=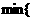
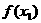 ,
,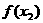 ,┅,
,┅,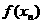
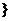 ;
;
当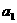 +
+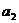 +┅+
+┅+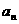 =0时,
=0时,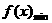 =
=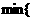
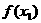 ,
,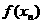
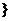 ,
,
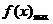 =
=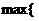
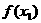 ,
,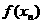
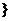 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com