22．(本小题满分14分)

如图所示，过抛物线x² = 4y的对称轴上任一点P ( 0 , m ) ( m＞0 )作直线抛物线交于A、B两点，点Q是点P关于原点的对称点。

(1)设点P分有向线段⊥(–)；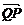

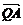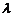
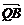(2)设直线AB的方程是x – 2y + 12 = 0 , 过A、B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程。

21．(本小题满分12分)

　　　 (理)已知函数f ( x ) = x² + alnx + 1 , ( a≠0 ) 。

　　　 (1)若f ( x )在区间 ( 0 ， 2 )上是减函数，求实数a的取值范围；

　　　 (2)函数y = f ( x )的图像上是否存在两条与直线y = 2x 平行或重合的切线，若存在，求出a的范围；若不存在，说明理由。

　　　 (文)已知a为实数，函数f ( x ) = (x² –4 )( x – a ).

　　　 (1)若函数y = f ( x ) 在 ( 0 , 2 )上是减函数a的取值范围；

　　　 (2)是否存在a的值，使y = f ( x )的切线与y = – 5x平行，若存在，求出a的值，若不存在，说明理由。

20．(本小题满分12分)

　　　 数列{a_n}的前n项和记为S_n，已知a₁ = 1 , a_n+1 =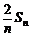( n≥1)

　　　 (1)求数列{a_n}的通项公式；

　　　 (2)设b_n = 2ⁿ·a_n ，求{b_n}的前n项和T_n 。

19．如图所示，已知直平行六面体ABCD-A₁B₁C₁D₁中AD⊥BD，AD = BD = a , E是CC₁的中点，A₁D⊥BE。　　　　　　　　　

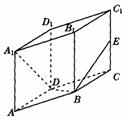　　　 (1)求证：A₁D⊥平面BDE ；

　　　 (2)求二面角E-BD-C的大小；

　　　 (3)求点B到平面A₁DE的距离。

18．(本小题满分12分)

　　　 波士顿 ( boston )的水位午夜12点是高潮位，水面高出海平面3.01 m，早晨低潮位，水面高出海平面0.01 m ；水位的变化呈周期性变化，试选择一个函数，描述水位的变化。

　　　 (1)写出函数的解析式；

　　　 (2)求出午后两点的水位。

17．(本小题满分12分)

　　　 解关于x的不等式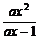：＞x 。

16．不等式| x –3 | + | y + 3 | ≤2围成的图形的面积是_____________。

15．(理)某新品的次品率为5%，今在这产品中抽查200件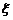，表示抽到的次品数，则E=__________ 。

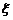　　　 (文)某校一年级有甲、乙两班，甲班有40人，乙班有50人。一次考试中，甲班的平均成绩是90分，乙班的平均成绩是不是81分，则该校一年级的平均成绩是____________。

14．f ( x ) sin⁴x –2sinx·cosx + cos⁴x , 则函数f ( x )的值域是_____________。

13．若函数f ( x )对任意实数x满足f ( x + 2 ) =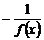 , 且f ( 1 ) = –5, 则f [f ( 5 )] =______。