
题目列表(包括答案和解析)
2.
已知点A(6,-4),B(1,2)、C(x,y),O为坐标原点,若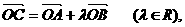 则点C的轨迹方程是
( )
则点C的轨迹方程是
( )
A.2x-y+16=0 B.2x-y-16=0 C.x-y+10=0 D.x-y-10=0
1. 直线l经过A(2,1)、B(1,m2)(m∈R)两点,那么直线l的倾斜角的取值范围是( )
A.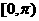 B.
B.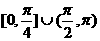 C.
C.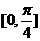 D.
D.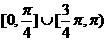
1 若向量
若向量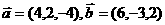 ,则
,则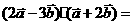 __________________
__________________
2 若向量
若向量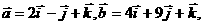 ,则这两个向量的位置关系是___________
,则这两个向量的位置关系是___________
3 已知向量
已知向量 ,若
,若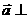
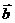 ,则
,则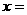 ______;若
______;若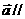
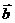 则
则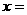 ______
______
4 已知向量
已知向量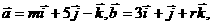 若
若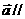
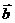 则实数
则实数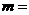 ______,
______,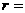 _______
_______
5 若
若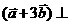
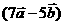 ,且
,且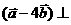
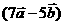 ,则
,则 与
与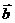 的夹角为____________
的夹角为____________
6 若
若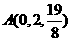 ,
,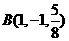 ,
,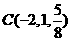 是平面
是平面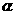 内的三点,设平面
内的三点,设平面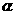 的法向量
的法向量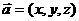 ,则
,则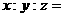 ________________
________________
7 已知空间四边形
已知空间四边形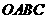 ,点
,点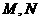 分别为
分别为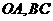 的中点,且
的中点,且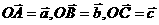 ,用
,用 ,
,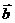 ,
,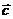 表示
表示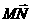 ,则
,则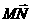 =_______________
=_______________
8 已知正方体
已知正方体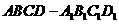 的棱长是
的棱长是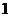 ,则直线
,则直线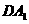 与
与 间的距离为
间的距离为 
(数学选修2-1)第三章 空间向量与立体几何
1 下列各组向量中不平行的是( )
下列各组向量中不平行的是( )
A
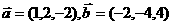 B
B
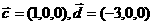
C
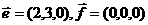 D
D
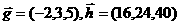
2 已知点
已知点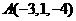 ,则点
,则点 关于
关于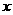 轴对称的点的坐标为( )
轴对称的点的坐标为( )
A
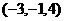 B
B
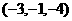 C
C
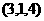 D
D
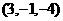
3 若向量
若向量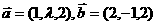 ,且
,且 与
与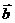 的夹角余弦为
的夹角余弦为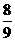 ,则
,则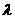 等于(
)
等于(
)
A
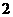 B
B
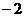 C
C
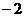 或
或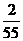 D
D
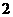 或
或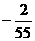
4 若A
若A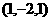 ,B
,B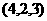 ,C
,C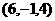 ,则△ABC的形状是( )
,则△ABC的形状是( )
A 不等边锐角三角形 B
不等边锐角三角形 B 直角三角形 C
直角三角形 C 钝角三角形
D
钝角三角形
D 等边三角形
等边三角形
5 若A
若A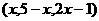 ,B
,B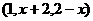 ,当
,当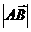 取最小值时,
取最小值时,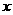 的值等于( )
的值等于( )
A
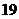 B
B
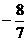 C
C
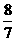 D
D
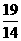
6 空间四边形
空间四边形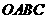 中,
中,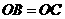 ,
,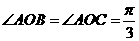 ,则
,则 <
<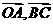 >的值是( )
>的值是( )
A
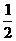 B
B
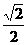 C
C -
-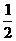 D
D

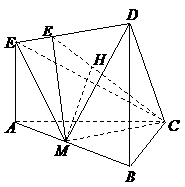
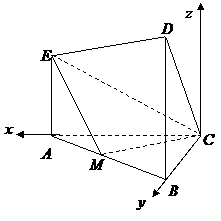
43.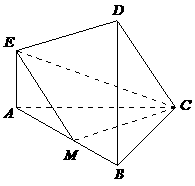 (浙江•理•19题)在如图所示的几何体中,
(浙江•理•19题)在如图所示的几何体中,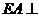 平面ABC,
平面ABC,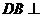 平面ABC,
平面ABC,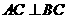 ,
,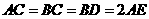 ,M是AB的中点。
,M是AB的中点。
(Ⅰ)求证: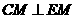 ;
;
(Ⅱ)求CM与平面CDE所成的角;
分析:本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.满分14分.
解答:
方法一:
(I)证明:因为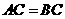 ,
,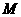 是
是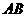 的中点,
的中点,
所以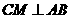 .
.
又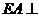 平面
平面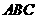 ,
,
所以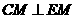 .
.
(II)解:过点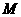 作
作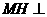 平面
平面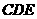 ,垂足是
,垂足是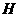 ,连结
,连结 交延长交
交延长交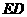 于点
于点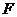 ,连结
,连结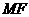 ,
, .
.
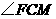 是直线
是直线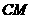 和平面
和平面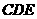 所成的角.
所成的角.
因为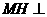 平面
平面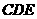 ,
,
所以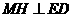 ,
,
又因为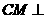 平面
平面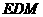 ,
,
所以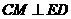 ,
,
则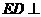 平面
平面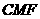 ,因此
,因此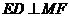 .
.
设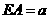 ,
,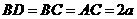 ,
,
在直角梯形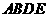 中,
中,
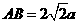 ,
,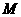 是
是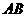 的中点,
的中点,
所以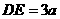 ,
,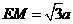 ,
,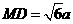 ,
,
得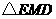 是直角三角形,其中
是直角三角形,其中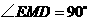 ,
,
所以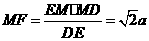 .
.
在 中,
中,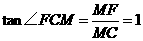 ,
,
所以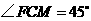 ,
,
故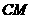 与平面
与平面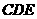 所成的角是
所成的角是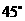 .
.
方法二:
如图,以点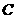 为坐标原点,以
为坐标原点,以 ,
,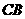 分别为
分别为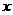 轴和
轴和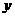 轴,过点
轴,过点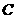 作与平面
作与平面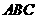 垂直的直线为
垂直的直线为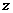 轴,建立直角坐标系
轴,建立直角坐标系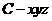 ,设
,设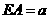 ,则
,则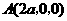 ,
,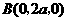 ,
,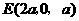 .
.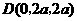 ,
,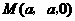 .
.
(I)证明:因为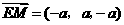 ,
,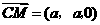 ,
,
所以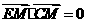 ,
,
故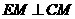 .
.
(II)解:设向量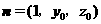 与平面
与平面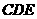 垂直,则
垂直,则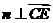 ,
,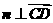 ,
,
 即
即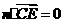 ,
,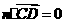 .
.
因为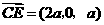 ,
,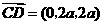 ,
,
所以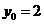 ,
,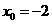 ,
,
即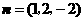 ,
,
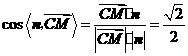 ,
,
直线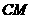 与平面
与平面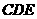 所成的角
所成的角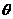 是
是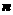 与
与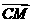 夹角的余角,
夹角的余角,
所以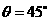 ,
,
因此直线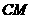 与平面
与平面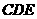 所成的角是
所成的角是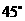 .
.
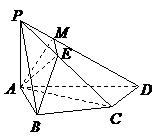
42. (天津•理•19题)如图,在四棱锥
(天津•理•19题)如图,在四棱锥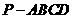 中,
中,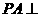 底面
底面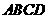 ,
,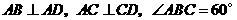 ,
,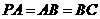 ,
,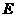 是
是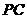 的中点.
的中点.
(Ⅰ)证明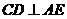 ;
;
(Ⅱ)证明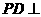 平面
平面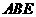 ;
;
(Ⅲ)求二面角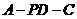 的大小;
的大小;
分析:本小题考查直线与直线垂直、直线与平面垂直、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.满分12分.
解答:(Ⅰ)证明:在四棱锥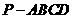 中,因
中,因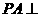 底面
底面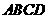 ,
,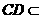 平面
平面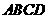 ,故
,故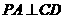 .
.
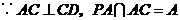 ,
, 平面
平面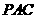 .
.
而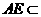 平面
平面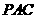 ,
,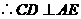 .
.
(Ⅱ)证明:由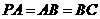 ,
,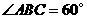 ,可得
,可得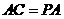 .
.
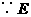 是
是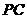 的中点,
的中点,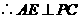 .
.
由(Ⅰ)知,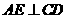 ,且
,且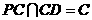 ,所以
,所以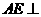 平面
平面 .
.
而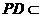 平面
平面 ,
,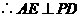 .
.
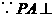 底面
底面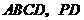 在底面
在底面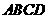 内的射影是
内的射影是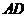 ,
,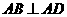 ,
,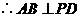 .
.
又 ,综上得
,综上得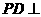 平面
平面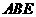 .
.
 (Ⅲ)解法一:过点
(Ⅲ)解法一:过点 作
作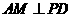 ,垂足为
,垂足为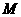 ,连结
,连结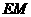 .则(Ⅱ)知,
.则(Ⅱ)知,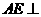 平面
平面 ,
,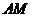 在平面
在平面 内的射影是
内的射影是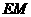 ,则
,则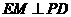 .
.
因此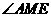 是二面角
是二面角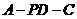 的平面角.
的平面角.
由已知,得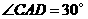 .设
.设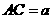 ,
,
可得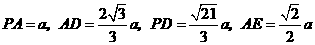 .
.
在 中,
中,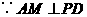 ,
,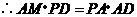 ,
,
则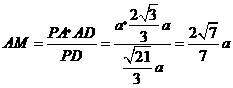 .在
.在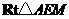 中,
中,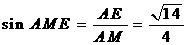 .
.
所以二面角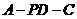 的大小是
的大小是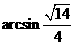 .
.
解法二:由题设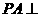 底面
底面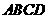 ,
,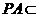 平面
平面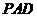 ,则平面
,则平面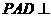 平面
平面 ,交线为
,交线为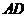 .
.
过点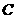 作
作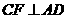 ,垂足为
,垂足为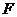 ,故
,故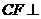 平面
平面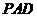 .过点
.过点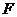 作
作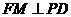 ,垂足为
,垂足为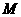 ,连结
,连结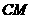 ,故
,故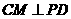 .因此
.因此 是二面角
是二面角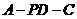 的平面角.
的平面角.
由已知,可得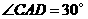 ,设
,设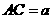 ,
,
可得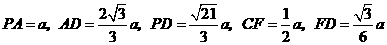 .
.
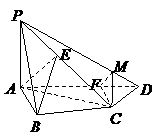
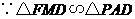 ,
,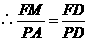 .
.
于是,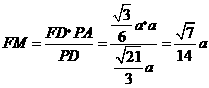 .
.
在 中,
中,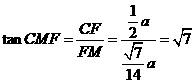 .
.
所以二面角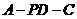 的大小是
的大小是 .
.
41.(四川•理•19题)如图,四边形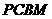 是直角梯形,∠
是直角梯形,∠ =90°,
=90°,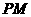 ∥
∥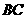 ,
,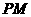 =1,
=1,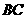 =2,又
=2,又 =1,∠
=1,∠ =120°,
=120°,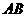 ⊥
⊥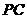 ,直线
,直线 与直线
与直线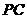 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面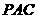 ⊥平面
⊥平面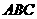 ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求三棱锥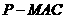 的体积;
的体积;
分析:本题主要考察异面直线所成的角、平面与平面垂直、二面角、三棱锥体积等有关知识,考察思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力。
解法一:
(Ⅰ)∵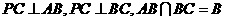
∴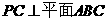 ,
,
又∵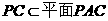
∴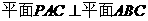
(Ⅱ)取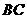 的中点
的中点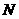 ,则
,则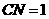 ,连结
,连结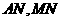 ,
,
∵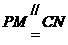 ,∴
,∴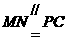 ,从而
,从而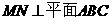
作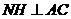 ,交
,交 的延长线于
的延长线于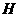 ,连结
,连结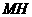 ,则由三垂线定理知,
,则由三垂线定理知,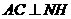 ,
,
从而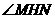 为二面角
为二面角 的平面角
的平面角
直线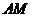 与直线
与直线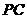 所成的角为
所成的角为
∴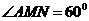
在 中,由余弦定理得
中,由余弦定理得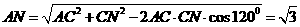
在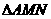 中,
中,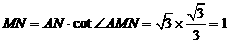
在 中,
中,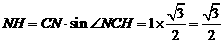
在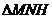 中,
中,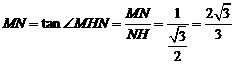
故二面角 的平面角大小为
的平面角大小为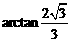
(Ⅲ)由(Ⅱ)知, 为正方形
为正方形
∴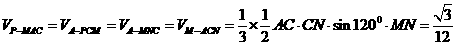
解法二:(Ⅰ)同解法一
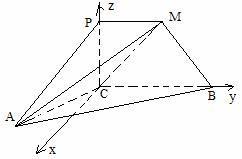 (Ⅱ)在平面
(Ⅱ)在平面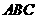 内,过
内,过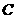 作
作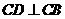 ,建立空间直角坐标系
,建立空间直角坐标系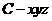 (如图)
(如图)
由题意有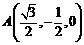 ,设
,设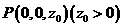 ,
,
则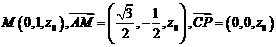
由直线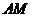 与直线
与直线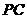 所成的解为
所成的解为 ,得
,得
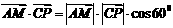 ,即
,即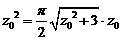 ,解得
,解得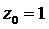
∴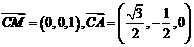 ,设平面
,设平面 的一个法向量为
的一个法向量为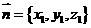 ,
,
则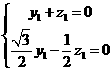 ,取
,取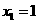 ,得
,得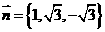
平面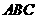 的法向量取为
的法向量取为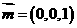
设 与
与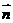 所成的角为
所成的角为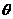 ,则
,则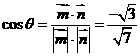
显然,二面角 的平面角为锐角,
的平面角为锐角,
故二面角 的平面角大小为
的平面角大小为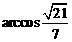
(Ⅲ)取平面 的法向量取为
的法向量取为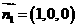 ,则点A到平面
,则点A到平面 的距离
的距离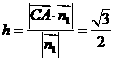
∵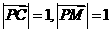 ,∴
,∴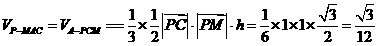
40.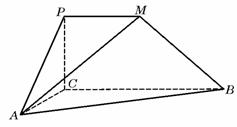 (上海•理•19题)体积为1的直三棱柱
(上海•理•19题)体积为1的直三棱柱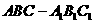 中,
中,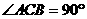 ,
,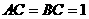 ,求直线
,求直线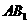 与平面
与平面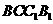 所成角。
所成角。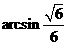
39.(陕西•理•19题)如图,在底面为直角梯形的四棱锥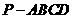 中
中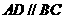 ,
,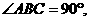
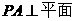
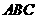 ,
,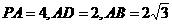 ,BC=6。
,BC=6。
(Ⅰ)求证: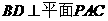 ;(Ⅱ)求二面角
;(Ⅱ)求二面角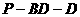 的大小;
的大小;
解法一:(Ⅰ)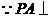 平面
平面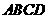 ,
,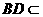 平面
平面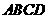 .
.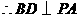 .
.
又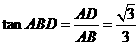 ,
,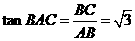 .
.
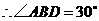 ,
,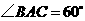 ,
,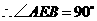 ,即
,即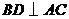 .
.
又 .
.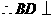 平面
平面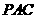 .
.
(Ⅱ)过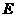 作
作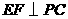 ,垂足为
,垂足为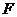 ,连接
,连接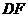 .
.
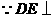 平面
平面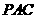 ,
,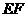 是
是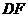 在平面
在平面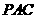 上的射影,由三垂线定理知
上的射影,由三垂线定理知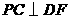 ,
,
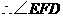 为二面角
为二面角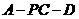 的平面角.
的平面角.
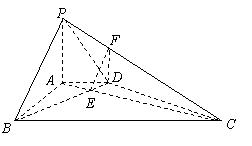 又
又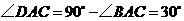 ,
,
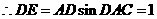 ,
,
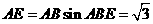 ,
,
又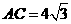 ,
,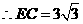 ,
,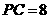 .
.
由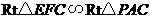 得
得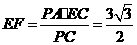 .
.
在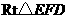 中,
中,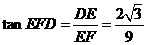 ,
,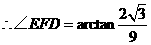 .
.
 二面角
二面角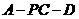 的大小为
的大小为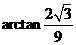 .
.
解法二:(Ⅰ)如图,建立坐标系,
则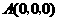 ,
,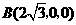 ,
,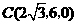 ,
,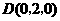 ,
,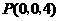 ,
,
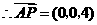 ,
,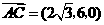 ,
,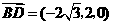 ,
,
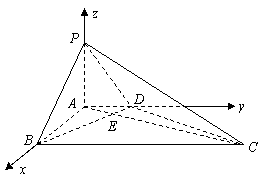
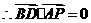 ,
,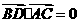 .
.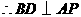 ,
,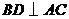 ,
,
又 ,
,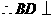 平面
平面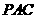 .
.
(Ⅱ)设平面 的法向量为
的法向量为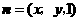 ,
,
则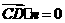 ,
,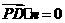 ,
,
又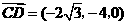 ,
,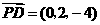 ,
,
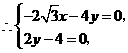 解得
解得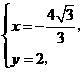
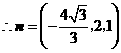
平面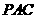 的法向量取为
的法向量取为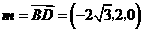 ,
,
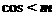 ,
,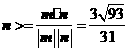 .
.
 二面角
二面角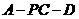 的大小为
的大小为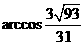 .
.
38.(宁夏•理•19题)如图,在三棱锥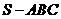 中,侧面
中,侧面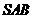 与侧面
与侧面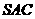 均为等边三角形,
均为等边三角形,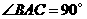 ,
, 为
为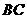 中点.
中点.
(Ⅰ)证明: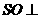 平面
平面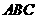 ;(Ⅱ)求二面角
;(Ⅱ)求二面角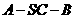 的余弦值.
的余弦值.
证明:
(Ⅰ)由题设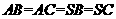

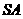 ,连结
,连结 ,
, 为等腰直角三角形,所以
为等腰直角三角形,所以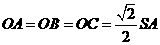 ,且
,且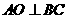 ,又
,又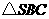 为等腰三角形,故
为等腰三角形,故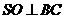 ,且
,且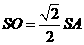 ,从而
,从而 .
.
所以 为直角三角形,
为直角三角形,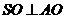 .
.
又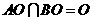 .
.
所以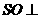 平面
平面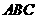 .
.
(Ⅱ)解法一:
取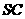 中点
中点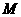 ,连结
,连结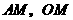 ,由(Ⅰ)知
,由(Ⅰ)知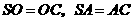 ,得
,得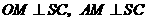 .
.
 为二面角
为二面角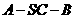 的平面角.
的平面角.
由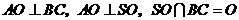 得
得 平面
平面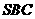 .
.
所以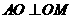 ,又
,又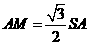 ,故
,故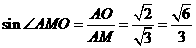 .
.
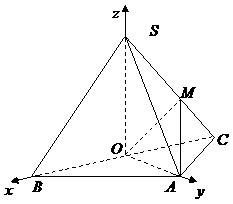 所以二面角
所以二面角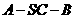 的余弦值为
的余弦值为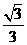 .
.
解法二:
以 为坐标原点,射线
为坐标原点,射线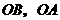 分别为
分别为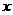 轴、
轴、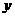 轴的正半轴,建立如图的空间直角坐标系
轴的正半轴,建立如图的空间直角坐标系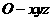 .
.
设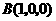 ,则
,则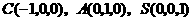 .
.
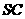 的中点
的中点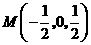 ,
,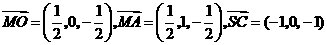 .
.
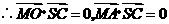 .
.
故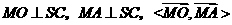 等于二面角
等于二面角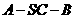 的平面角.
的平面角.
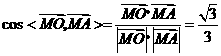 ,
,
所以二面角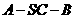 的余弦值为
的余弦值为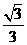 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com