
题目列表(包括答案和解析)
10、已知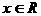 ,[x]表示不大于x的最大整数,如
,[x]表示不大于x的最大整数,如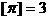 ,
,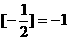 ,
,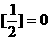 ,则
,则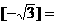 _____________;使
_____________;使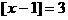 成立的x的取值范围是_____________ 答案:2
成立的x的取值范围是_____________ 答案:2
9、在实数的原有运算法则中,我们补充定义新运算“ ”如下:
”如下:
当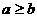 时,
时,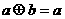 ;
;
当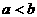 时,
时,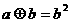 。
。
则函数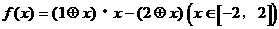 的最大值等于( C
)
的最大值等于( C
)
(“·”和“-”仍为通常的乘法和减法)A. 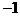 B.
1 C.
6 D.
12
B.
1 C.
6 D.
12
8、已知两个函数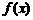 和
和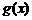 的定义域和值域都是集合{1,2,3},其定义如下表.
的定义域和值域都是集合{1,2,3},其定义如下表.
|
x |
1 |
2 |
3 |
|
f(x) |
2 |
3 |
1 |
|
x |
1 |
2 |
3 |
|
g(x) |
1 |
3 |
2 |
填写下列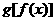 的表格,其三个数依次为
的表格,其三个数依次为
|
x |
1 |
2 |
3 |
|
g
(f(x)) |
|
|
|
A. 3,1,2 B . 2,1,3 C. 1,2,3 D. 3,2,1
答案:D
7、在△ABC中,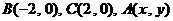 ,给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
,给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
|
条件 |
方程 |
|
①△ABC周长为10 |
 : :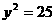 |
|
②△ABC面积为10 |
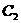 : :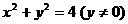 |
|
③△ABC中,∠A=90° |
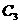 : :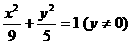 |
则满足条件①、②、③的轨迹方程分别为
(用代号 、
、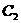 、
、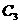 填入)
填入)
答案: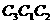
6、一个计算装置有一个入口A和一输出运算结果的出口B,将自然数列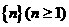 中的各数依次输入A口,从B口得到输出的数列
中的各数依次输入A口,从B口得到输出的数列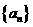 ,结果表明:①从A口输入
,结果表明:①从A口输入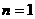 时,从B口得
时,从B口得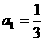 ;②当
;②当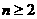 时,从A口输入
时,从A口输入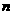 ,从B口得到的结果
,从B口得到的结果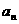 是将前一结果
是将前一结果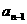 先乘以自然数列
先乘以自然数列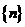 中的第
中的第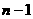 个奇数,再除以自然数列
个奇数,再除以自然数列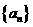 中的第
中的第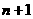 个奇数。试问:
个奇数。试问:
(1) 从A口输入2和3时,从B口分别得到什么数?
(2) 从A口输入100时,从B口得到什么数?并说明理由。
解(1)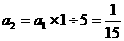
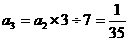
(2)先用累乖法得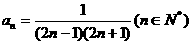
得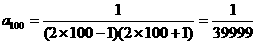
5、下面的一组图形为某一四棱锥S-ABCD的侧面与底面。
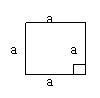
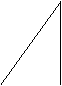

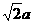
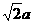
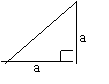
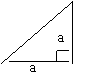
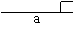
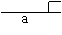
(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA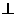 面ABCD,E为AB中点,求二面角E-SC-D的大小;
面ABCD,E为AB中点,求二面角E-SC-D的大小;
(3)求点D到面SEC的距离。
(1)存在一条侧棱垂直于底面(如图)………………3分
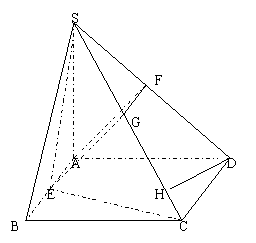 证明:
证明: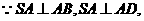 且AB、AD是面ABCD内的交线
且AB、AD是面ABCD内的交线 SA
SA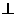 底面ABCD……………………5分
底面ABCD……………………5分
(2)分别取SC、SD的中点G、F,连GE、GF、FA,
则GF//EA,GF=EA, AF//EG
AF//EG
而由SA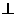 面ABCD得SA
面ABCD得SA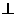 CD,
CD,
又AD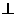 CD,
CD, CD
CD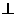 面SAD,
面SAD,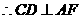
又SA=AD,F是中点,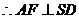
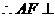 面SCD,EG
面SCD,EG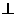 面SCD,
面SCD,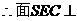 面SCD
面SCD
所以二面角E-SC-D的大小为90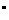 …………10分
…………10分
(3)作DH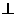 SC于H,
SC于H,
 面SEC
面SEC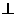 面SCD,
面SCD, DH
DH 面SEC,
面SEC,
 DH之长即为点D到面SEC的距离,12分
DH之长即为点D到面SEC的距离,12分
 在Rt
在Rt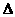 SCD中,
SCD中,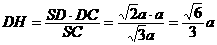
答:点D到面SEC的距离为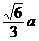 ………………………14分
………………………14分
4、若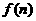 为
为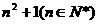 的各位数字之和,如:
的各位数字之和,如: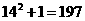 ,
,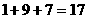 ,则
,则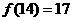 ;记
;记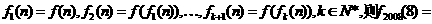 ____
____
答案:5
3、10.定义一种运算“*”:对于自然数n满足以下运算性质:
(i)1*1=1,(ii)(n+1)*1=n*1+1,则n*1等于
A.n
B.n+1
C.n -1
D.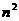 答案:D
答案:D
2、用类比推理的方法填表
等差数列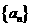 中 中 |
等比数列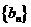 中 中 |
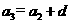 |
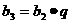 |
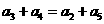 |
 |
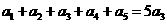 |
|
答案: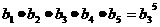
1、(Ⅰ)已知函数: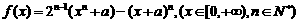 求函数
求函数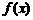 的最小值;
的最小值;
(Ⅱ)证明: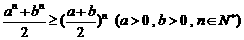 ;
;
(Ⅲ)定理:若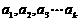 均为正数,则有
均为正数,则有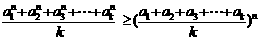 成立
成立
(其中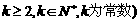 .请你构造一个函数
.请你构造一个函数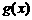 ,证明:
,证明:
当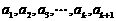 均为正数时,
均为正数时,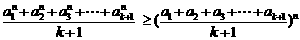 .
.
解:(Ⅰ)令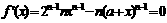 得
得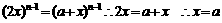 …2分
…2分
当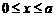 时,
时,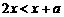
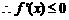 故
故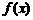 在
在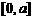 上递减.
上递减.
当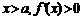 故
故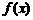 在
在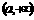 上递增.所以,当
上递增.所以,当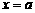 时,
时,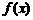 的最小值为
的最小值为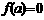 .….4分
.….4分
(Ⅱ)由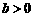 ,有
,有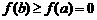 即
即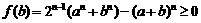
故 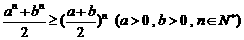 .………………………………………5分
.………………………………………5分
(Ⅲ)证明:要证: 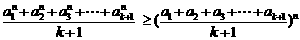
只要证: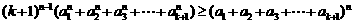
设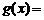
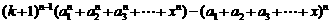 …………………7分
…………………7分
则
令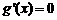 得
得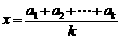 …………………………………………………….8分
…………………………………………………….8分
当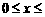
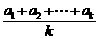 时,
时,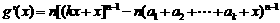
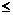
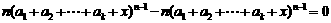
故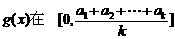 上递减,类似地可证
上递减,类似地可证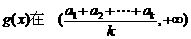 递增
递增
所以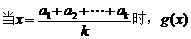 的最小值为
的最小值为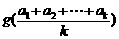 ………………10分
………………10分
而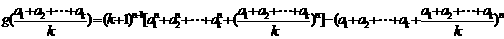
=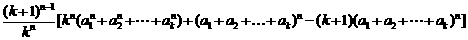
=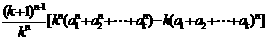 =
=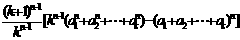
由定理知: 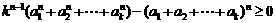 故
故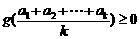
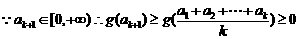
故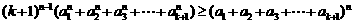
即: 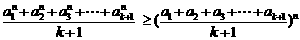 .…………………………..14分
.…………………………..14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com