
题目列表(包括答案和解析)
1. 给出直线的方向向量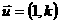 或
或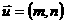 ,等于已知直线的斜率
,等于已知直线的斜率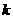 或
或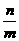 ;
;
4.在抛物线y2=4x上恒有两点关于y=kx+3对称,求k范围.
解:设B、C关于直线y=kx+3对称,则BC方程为x=-ky+m,代入 y2=4x 得 y2+4ky-4m=0 设B(x, y), C(x2,
y2), BC中点M(x0, y0), ∴ 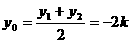 , x0=2k2+m,∵ M(x0, y0)在l上,∴
-2k=k(2k2+m)+3
∴
, x0=2k2+m,∵ M(x0, y0)在l上,∴
-2k=k(2k2+m)+3
∴ 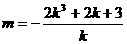 , 又BC与抛物线交于两点,∴Δ=16k2+16m>0, 即
, 又BC与抛物线交于两点,∴Δ=16k2+16m>0, 即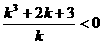 ,
,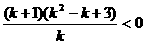 解得-1<k<0.
解得-1<k<0.
3.直线l: 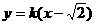 与曲线x2-y2=1(x>0)相交于A,B两点,则直线l的倾角为(
).
与曲线x2-y2=1(x>0)相交于A,B两点,则直线l的倾角为(
).
A、[0,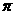 ) B、
) B、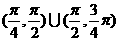 C、
C、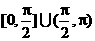 D、
D、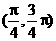
分析:直线与双曲线右支交于两点,不能仅仅用Δ判定,
x2-k2(x2-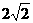 x+2)=1 (1-k2)x2+
x+2)=1 (1-k2)x2+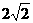 k2x-2k2-1=0
k2x-2k2-1=0
∴ 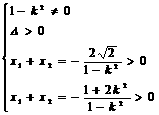 ∴ k>1 或 k<-1. ∴ 倾角
∴ k>1 或 k<-1. ∴ 倾角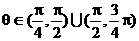 ,选B.
,选B.
2.直线y:kx+1与椭圆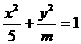 恒有公共点,则m的取值范围是( ).
恒有公共点,则m的取值范围是( ).
A、m≥1且m≠5 B、m≥1 C、m≠5 D、m≤5
分析:直线与椭圆恒有公共点Û联立方程Δ恒大于等于0,
由Δ≥0恒成立可得 m≥1-5k2恒成立,∴ m≥(1-5k2)max, ∴m≥1且m≠5,选A.
1.过点(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有( ).
A、一条 B、两条 C、三条 D、四条
分析:首先注意点(2,4)在抛物线上,其次只有一个公共点,包括直线平行于抛物线的对称轴,与抛物线交于一点,因而选B.
5.交轨法
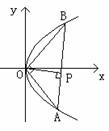 例:抛物线y2=2px(p>0),O为坐标原点,A、B在抛物线上,且OA⊥OB,过O作OP⊥AB交AB于P,求P点轨迹方程.
例:抛物线y2=2px(p>0),O为坐标原点,A、B在抛物线上,且OA⊥OB,过O作OP⊥AB交AB于P,求P点轨迹方程.
解:设OA=y=kx, 则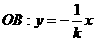 ,
,
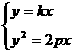 得
得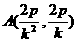 同理 B(2pk2, -2pk)
同理 B(2pk2, -2pk)
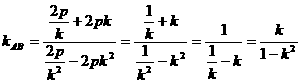
AB: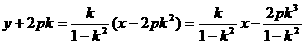
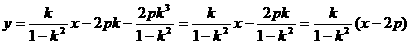 ....①
....①
而op: 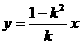 .....②
.....②
∵ P为AB与OP的交点,联立①②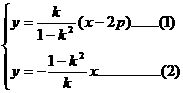 (1)×(2)消去k,
(1)×(2)消去k,
y2=-(x-2p)x, ∴ x2+y2-2px=0(x≠0)即为所求.
4.直接法(直接利用曲线定义)
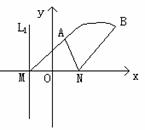 例:如图,直线l1, l2相交于M,l1⊥l2,点N∈l1, 以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等,若ΔAMN为锐角Δ,
例:如图,直线l1, l2相交于M,l1⊥l2,点N∈l1, 以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等,若ΔAMN为锐角Δ,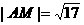 , |AN|=3,|BN|=6,建立适当坐标系,求曲线段C的方程.
, |AN|=3,|BN|=6,建立适当坐标系,求曲线段C的方程.
分析:以l1为x轴,以MN的中垂线为y轴建立直角坐标系,如图.
由题意,曲线段C是以N为焦点,以l2为准线的抛物线的一部分,
其中A、B分别为C的端点.
由已知条件,可求方程为y2=8x(1≤x≤4, y>0)(过程略)
3.直接法(直接到方程化简)
例:设点O为原点,点M在直线l: x=-p(p>0)上移动,动点N在线段MO的延长线上,且满足|MN|=|MO|·|NO|. 求动点N的轨迹方程.
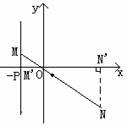 解:设N坐标为(x, y),过N作NN'⊥x轴于N',
解:设N坐标为(x, y),过N作NN'⊥x轴于N',
∵ M,O,N共线,
∴ 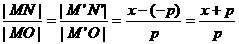 , 由已知 |MN|=|MO|·|NO|
, 由已知 |MN|=|MO|·|NO|
∴ 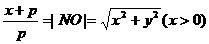
∴ 所求方程为(p2-1)x2+p2y2-2px-p2=0(x>0)
2.相关点求轨迹法(代入法)
例:设抛物线过定点A(0,2),且以x轴为准线求抛物线顶点M的轨迹C的方程.
分析:A(0,2)在抛物线上,体现为
①A(0,2)的坐标满足曲线方程
②A(0,2)满足曲线定义
在本题中以方式②为佳,设M(x, y),焦点F(x0, y0),
∵ |AF|=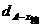 ,∴
,∴ 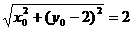 , ∴
, ∴ 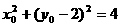 ......①
......①
而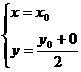 , ∴
, ∴ 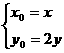 代入① ∴ x2+(2y-2)2=4,
代入① ∴ x2+(2y-2)2=4, 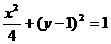 且 y≠0.
且 y≠0.
1.待定系数法
例:已知椭圆D: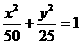 与圆:x2+(y-m)2=9(m∈R),双曲线G与椭圆D有相同焦点,它的两条渐近线恰好与圆M相切.1)当m=5时,求双曲线G的方程.
与圆:x2+(y-m)2=9(m∈R),双曲线G与椭圆D有相同焦点,它的两条渐近线恰好与圆M相切.1)当m=5时,求双曲线G的方程.
2)当m取何值时,双曲线的两条准线间的距离为1.
解:1)椭圆D的两个焦点F1(-5,0),F2(5,0),因而双曲线中心在原点,焦点在x轴上,且c=5.
设双曲线G的方程为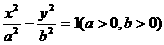 ∴ 渐近线为bx±ay=0且a2+b2=25,
∴ 渐近线为bx±ay=0且a2+b2=25,
m=5时,圆心M(0,5), r=3.∴ 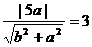 , 得 a=3, b=4, ∴G方程为
, 得 a=3, b=4, ∴G方程为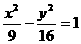 .
.
2)双曲线两准线间距离为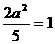 , ∴
, ∴ 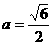 ,
,
∵ G的渐近线与M相切, ∴ 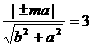 ,∴
,∴ 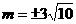 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com