
题目列表(包括答案和解析)
1.椭圆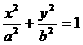 (a>b>0)的左焦点F到过顶点A(-a, 0), B(0,b)的直线的距离等于
(a>b>0)的左焦点F到过顶点A(-a, 0), B(0,b)的直线的距离等于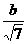 ,则椭圆的离心率为( ).
,则椭圆的离心率为( ).
A、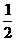 B、
B、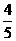 C、
C、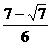 D、
D、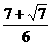
分析:本题条件不易用平面几何知识转化,因而过A、B的方程为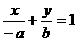 ,左焦点F(-c,0),则
,左焦点F(-c,0),则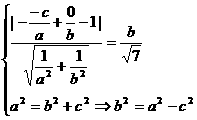 ,化简,得5a2-14ac+8c2=0
得
,化简,得5a2-14ac+8c2=0
得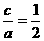 或
或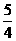 (舍), ∴ 选A.
(舍), ∴ 选A.
小结:应熟悉各方程的标准形式及各参数之间的关系和几何意义.若题面改为“双曲线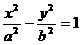 (a>b>0)”,则由“a>b>0”这个隐含条件可知离心率e的范围限制,即a>b>0,∴ a2>b2, ∴a2>c2-a2
从而
(a>b>0)”,则由“a>b>0”这个隐含条件可知离心率e的范围限制,即a>b>0,∴ a2>b2, ∴a2>c2-a2
从而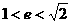 .
.
19、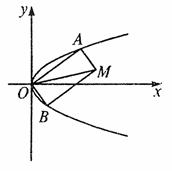 过抛物线
过抛物线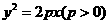 的顶点O作两点互相垂直
的顶点O作两点互相垂直
的弦 、
、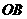 ,再以
,再以 、
、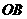 为邻边作矩形
为邻边作矩形 ,
,
如图.求点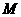 的轨迹方程.
的轨迹方程.
18、已知曲线C满足方程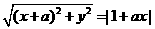 (
(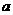 >0为常数)。
>0为常数)。
(1) 判断曲线的形状。
(2) 若直线L:y=x+a交曲线C于点P、Q,线段PQ中点的横坐标为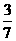 ,试问在曲线C上是否存在不同的两点A、B关于直线L对称?
,试问在曲线C上是否存在不同的两点A、B关于直线L对称?
17、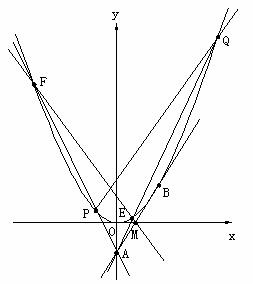 如图:自点A(0,-1)向抛物线
如图:自点A(0,-1)向抛物线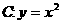 作切线AB,切点为B,且点B在第一象限,再过线段AB的中点M作直线
作切线AB,切点为B,且点B在第一象限,再过线段AB的中点M作直线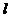 与抛物线C交于不同的两点E、F,直线AF、AE分别交抛物线C于P、Q两点。
与抛物线C交于不同的两点E、F,直线AF、AE分别交抛物线C于P、Q两点。
(I)求切线AB的方程及切点B的坐标;
(II)证明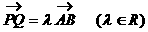
16、已知直线L: 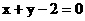 与抛物线 C:
与抛物线 C: 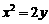 相交于点A、B
相交于点A、B
(Ⅰ)求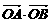 .
.
(Ⅱ)在抛物线 C上求一点P,使P点在L的下方且到直线L的距离最大.
15.双曲线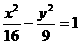 右支上的点P到左焦点的距离为9,则点P的坐标为_________.
右支上的点P到左焦点的距离为9,则点P的坐标为_________.
14、已知双曲线
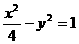 的实轴为
的实轴为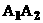 ,虚轴为
,虚轴为 ,将坐标平面沿
,将坐标平面沿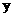 轴折起,使双
轴折起,使双
曲线的右焦点F2折至点F,若点F在平面A1B1B2内的射影恰好是该双曲线的左顶点
A1,则直线B1F与平面A1B1B2所成角的正切值为
13、设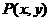 是曲线
是曲线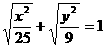 上的点,F1(-4,0),F2(4,0),则:
上的点,F1(-4,0),F2(4,0),则:
A.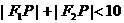 B.
B.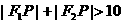
C.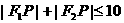 D.
D.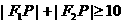
12、中心在原点,准线方程为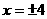 ,离心率为
,离心率为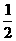 的椭圆方程是
的椭圆方程是
A.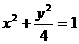 B.
B.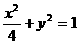 C.
C.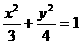 D.
D.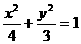
11、椭圆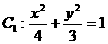 的左准线为l,左、右焦点分别为F1,F2,抛物线C2的准线为l,焦点是F2,C1与C2的一个交点为P,则|PF2|的值等于:
的左准线为l,左、右焦点分别为F1,F2,抛物线C2的准线为l,焦点是F2,C1与C2的一个交点为P,则|PF2|的值等于:
A.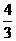 B.
B.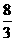 C.4 D.8
C.4 D.8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com