
题目列表(包括答案和解析)
18.(本小题满分12分)
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件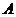 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率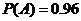 .
.
(1)求从该批产品中任取1件是二等品的概率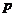 ;
;
 (2)若该批产品共100件,从中任意抽取2件,
(2)若该批产品共100件,从中任意抽取2件, 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求 的分布列.
的分布列.
14.在某项测量中,测量结果 服从正态分布
服从正态分布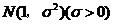 .若
.若 在
在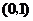 内取值的概率为0.4,则
内取值的概率为0.4,则 在
在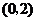 内取值的概率为
.0.8
内取值的概率为
.0.8
12.设集合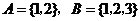 ,分别从集合
,分别从集合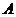 和
和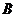 中随机取一个数
中随机取一个数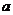 和
和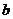 ,确定平面上的一个点
,确定平面上的一个点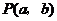 ,记“点
,记“点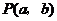 落在直线
落在直线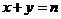 上”为事件
上”为事件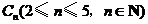 ,若事件
,若事件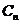 的概率最大,则
的概率最大,则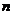 的所有可能值为( )
的所有可能值为( )
A.3 B.4 C.2和5 D.3和4
全国II理
18.(本小题满分12分)
解:(Ⅰ)记“该选手能正确回答第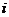 轮的问题”的事件为
轮的问题”的事件为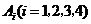 ,则
,则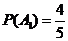 ,
,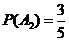 ,
,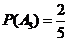 ,
,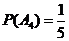 ,
, 该选手进入第四轮才被淘汰的概率
该选手进入第四轮才被淘汰的概率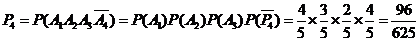 .
.
(Ⅱ)该选手至多进入第三轮考核的概率
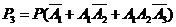
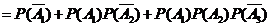
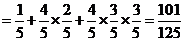 .
.
 山东理
山东理
(8)某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒; 第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为
第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为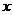 ,成绩大于等于15秒且小于17秒的学生人数为
,成绩大于等于15秒且小于17秒的学生人数为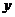 ,则从频率分布直方图中可分析出
,则从频率分布直方图中可分析出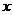 和
和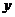 分别为( )
分别为( )
A.0.9,35 B.0.9,45
C.0.1,35 D.0.1,45
(12)位于坐标原点的一个质点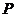 按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是
按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是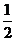 ,质点
,质点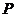 移动五次后位`于点
移动五次后位`于点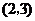 的概率是( )
的概率是( )
A.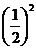 B.
B.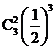 C.
C.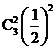 D.
D.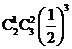
(18)(本小题满分12分)
设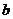 和
和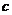 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量 表示方程
表示方程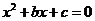 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程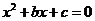 有实根的概率;
有实根的概率;
(Ⅱ)求 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程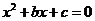 有实根的概率.
有实根的概率.
[标准答案]:(I)基本事件总数为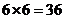 ,
,
若使方程有实根,则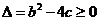 ,即
,即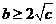 。
。
当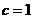 时,
时,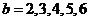 ;
;
当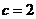 时,
时,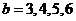 ;
;
当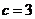 时,
时,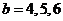 ;
;
当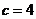 时,
时,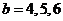 ;
;
当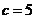 时,
时,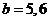 ;
;
当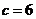 时,
时,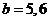 ,
,
目标事件个数为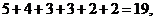
因此方程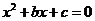 有实根的概率为
有实根的概率为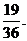
(II)由题意知,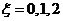 ,则
,则
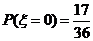 ,
,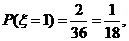
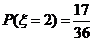 ,
,
故 的分布列为
的分布列为
 |
0 |
1 |
2 |
|
P |
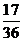 |
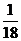 |
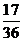 |
 的数学期望
的数学期望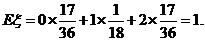
(III)记“先后两次出现的点数中有5”为事件M,“方程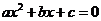 有实根” 为事件N,则
有实根” 为事件N,则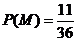 ,
,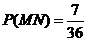 ,
,
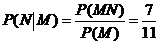 .
.
山东文
18.(本小题满分12分)
某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则
即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为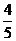 、
、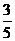 、
、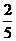 、
、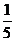 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手进入第四轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率.
(注:本小题结果可用分数表示)
6.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是
(A)4 (B)5 (C)6 (D)7
18.(本小题满分12分)
解法一:(Ⅰ)记“该选手能正确回答第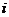 轮的问题”的事件为
轮的问题”的事件为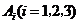 ,则
,则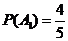 ,
,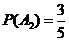 ,
,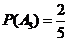 ,
,
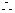 该选手被淘汰的概率
该选手被淘汰的概率
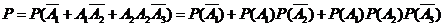
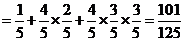 .
.
(Ⅱ) 的可能值为
的可能值为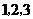 ,
,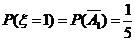 ,
,
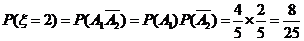 ,
,
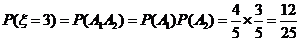 .
.
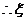 的分布列为
的分布列为
 |
1 |
2 |
3 |
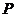 |
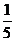 |
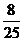 |
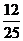 |
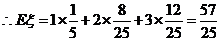 .
.
解法二:(Ⅰ)记“该选手能正确回答第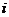 轮的问题”的事件为
轮的问题”的事件为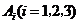 ,则
,则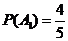 ,
,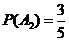 ,
,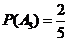 .
.
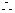 该选手被淘汰的概率
该选手被淘汰的概率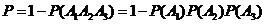
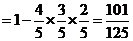 .
.
(Ⅱ)同解法一.
陕西文
18.(本小题满分12分)
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为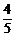 、
、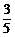 、
、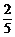 ,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数数期望.(注:本小题结果可用分数表示)
9.在五个数字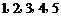 中,若随机取出三个数字,则剩下两个数字都是奇数的概率是
中,若随机取出三个数字,则剩下两个数字都是奇数的概率是
(结果用数值表示).0.3
陕西文
18.本小题主要考查互斥事件、相互独立事件、离散型随机变量的分布列和数学期望等基础知识,考查运用概率知识解决实际问题的能力.满分12分.
(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件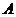 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件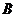 .由于事件
.由于事件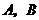 相互独立,且
相互独立,且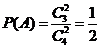 ,
,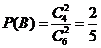 .
.
故取出的4个球均为黑球的概率为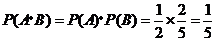 .
.
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件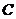 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件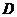 .由于事件
.由于事件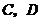 互斥,
互斥,
且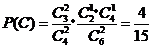 ,
,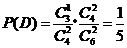 .
.
故取出的4个球中恰有1个红球的概率为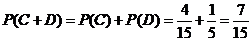 .
.
(Ⅲ)解: 可能的取值为
可能的取值为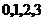 .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得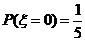 ,
,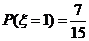 ,
,
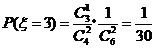 .从而
.从而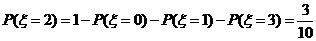 .
.
 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
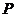 |
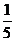 |
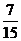 |
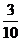 |
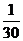 |
 的数学期望
的数学期望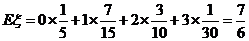 .
.
天津文
(11)从一堆苹果中任取了20只,并得到它们的质量(单位:克)数据分布表如下:
|
分组 |
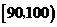 |
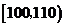 |
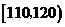 |
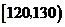 |
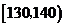 |
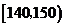 |
|
频数 |
1 |
2 |
3 |
10 |
|
1 |
则这堆苹果中,质量不小于120克的苹果数约占苹果总数的 %.70
(18)(本小题满分12分)
已知甲盒内有大小相同的3个红球和4个黑球,乙盒内有大小相同的5个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为红球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(18)本小题主要考查互斥事件、相互独立事件等概率的基础知识,考查运用概率知识解决实际问题的能力.满分12分.
(Ⅰ)解:设“从甲盒内取出的2个球均为红球”为事件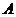 ,“从乙盒内取出的2个球均为红球”为事件
,“从乙盒内取出的2个球均为红球”为事件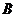 .由于事件
.由于事件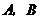 相互独立,且
相互独立,且
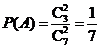 ,
,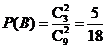 ,
,
故取出的4个球均为红球的概率是
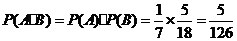 .
.
(Ⅱ)解:设“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个红球为黑球”为事件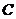 ,“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件
,“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件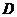 .由于事件
.由于事件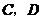 互斥,且
互斥,且
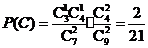 ,
,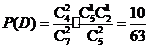 .
.
故取出的4个红球中恰有4个红球的概率为
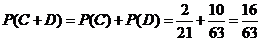 .
.
浙江理
(5)已知随机变量 服从正态分布
服从正态分布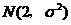 ,
,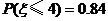 ,则
,则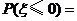 ( )
( )
A.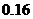 B.
B.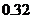 C.
C.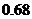 D,
D,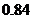
(15)随机变量 的分布列如下:
的分布列如下:

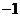
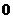
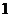
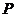
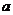
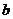
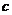
其中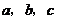 成等差数列,若
成等差数列,若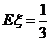 ,则
,则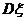 的值是
.
的值是
.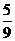
浙江文
(8)甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜.根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是
(A1 0.216 (B)0.36 (C)0.432 (D)0.648
(13)某校有学生2000人,其中高三学生500人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高三学生的人数为___________.50
上海文
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com