
题目列表(包括答案和解析)
20.(本小题共14分)
已知函数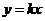 与
与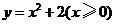 的图象相交于
的图象相交于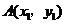 ,
, ,
,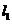 ,
,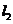 分别是
分别是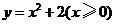 的图象在
的图象在 两点的切线,
两点的切线,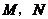 分别是
分别是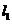 ,
,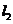 与
与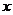 轴的交点.
轴的交点.
(I)求 的取值范围;
的取值范围;
(II)设 为点
为点 的横坐标,当
的横坐标,当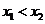 时,写出
时,写出 以
以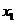 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(III)试比较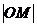 与
与 的大小,并说明理由(
的大小,并说明理由(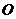 是坐标原点).
是坐标原点).
19.(本小题共14分)
 如图,矩形
如图,矩形 的两条对角线相交于点
的两条对角线相交于点 ,
,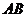 边所在直线的方程为
边所在直线的方程为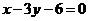 点
点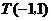 在
在 边所在直线上.
边所在直线上.
(I)求 边所在直线的方程;
边所在直线的方程;
(II)求矩形 外接圆的方程;
外接圆的方程;
(III)若动圆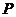 过点
过点 ,且与矩形
,且与矩形 的外接圆外切,求动圆
的外接圆外切,求动圆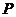 的圆心的轨迹方程.
的圆心的轨迹方程.
18.(本小题共12分)
某条公共汽车线路沿线共有11个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有6位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
(I)这6位乘客在其不相同的车站下车的概率;
(II)这6位乘客中恰有3人在终点站下车的概率;
17.(本小题共14分)
如图,在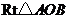 中,
中, ,斜边
,斜边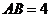 .
. 可以通过
可以通过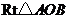 以直线
以直线 为轴旋转得到,且二面角
为轴旋转得到,且二面角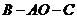 的直二面角.
的直二面角.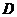 是
是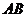 的中点.
的中点.
(I)求证:平面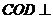 平面
平面 ;
;
(II)求异面直线 与
与 所成角的大小.
所成角的大小.
16.(本小题共13分)
数列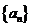 中,
中,
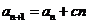 (
(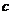 是常数,
是常数, ),且
),且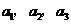 成公比不为
成公比不为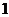 的等比数列.
的等比数列.
 (I)求
(I)求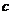 的值;
的值;
(II)求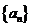 的通项公式.
的通项公式.
15.(本小题共12分)
记关于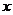 的不等式
的不等式 的解集为
的解集为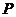 ,不等式
,不等式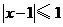 的解集为
的解集为 .
.
(I)若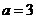 ,求
,求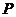 ;
;
(II)若 ,求正数
,求正数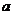 的取值范围.
的取值范围.
14.已知函数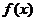 ,
, 分别由下表给出
分别由下表给出
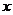 |
1 |
2 |
3 |
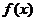 |
2 |
1 |
1 |
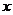 |
1 |
2 |
3 |
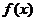 |
3 |
2 |
1 |
则 的值为 ;当
的值为 ;当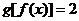 时,
时,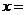 .
.
13.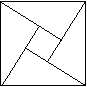 2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为
2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为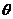 ,那么
,那么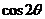 的值等于 .
的值等于 .
12.在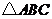 中,若
中,若 ,
,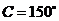 ,
,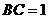 ,则
,则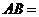 .
.
11.已知向量 .若向量
.若向量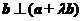 ,则实数
,则实数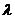 的值是 .
的值是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com