
题目列表(包括答案和解析)
4、“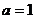 ”是“函数
”是“函数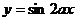 的最小正周期为
的最小正周期为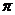 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3、满足“对任意实数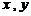 ,
,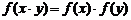 都成立”的函数可以是
( )
都成立”的函数可以是
( )
A.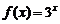 ; B.
; B. 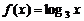 ; C.
; C.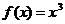 ; D.
; D.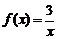
2、若复数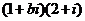 是纯虚数(
是纯虚数(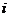 是虚数单位,
是虚数单位,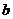 是实数),则
是实数),则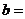 ( )
( )
(A)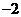 (B)
(B)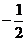 (C)
(C)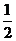 (D)2
(D)2
1、设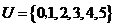 ,
,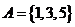 ,
,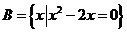 ,则
,则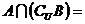 ( )
( )
A.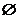 B.
B.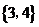 C.
C.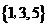 D.
D.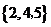
22.(本小题满分12分)
数列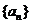 中,
中,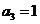 ,
,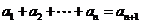 (
(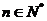 )。
)。
(Ⅰ)求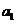 ,
,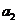 ,
,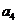 ,
,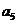 ;
;
(Ⅱ)求数列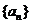 的前
的前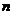 项和
项和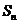 ;
;
(Ⅲ)设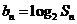 ,存在数列
,存在数列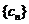 使得
使得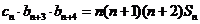 ,试求数列
,试求数列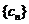 的前
的前 项和
项和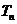 .
.
21.(本小题满分14分)
己知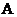 、
、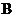 、
、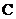 是椭圆
是椭圆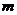 :
: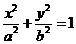 (
(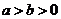 )上的三点,其中点
)上的三点,其中点 的坐标为
的坐标为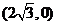 ,
,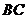 过椭圆的中心,且
过椭圆的中心,且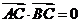 ,
,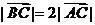 。
。
(Ⅰ)求椭圆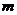 的方程;
的方程;
(Ⅱ)过点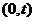 的直线
的直线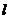 (斜率存在时)与椭圆
(斜率存在时)与椭圆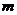 交于两点
交于两点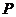 ,
,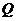 ,设
,设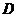 为椭圆
为椭圆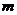 与
与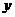 轴负半轴的交点,且
轴负半轴的交点,且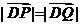 ,求实数
,求实数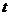 的取值范围.
的取值范围.
20.(本小题满分12分)
设函数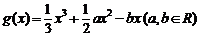 ,在其图象上一点P(x,y)处的切线的斜率记为
,在其图象上一点P(x,y)处的切线的斜率记为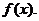
(Ⅰ)若方程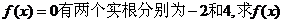 的表达式;
的表达式;
(Ⅱ)若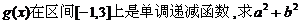 的最小值。
的最小值。
18.(本小题满分12分)
某班甲、乙两学生的高考备考成绩如下:
甲: 512 554 528 549 536 556 534 541 522 538
乙:515 558 521 543 532 559 536 548 527 531
(Ⅰ)用茎叶图表示两学生的成绩;
(Ⅱ)分别求两学生成绩的中位数和平均分.
.19.(本小题满分12分)
已知如图(1),梯形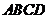 中,
中,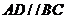 ,
,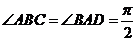 ,
,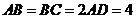 ,
,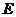 、
、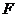 分别是
分别是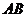 、
、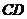 上的动点,且
上的动点,且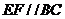 ,设
,设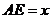 (
(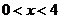 )。沿
)。沿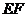 将梯形
将梯形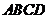 翻折,使平面
翻折,使平面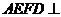 平面
平面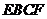 ,如图(2)。
,如图(2)。
(Ⅰ)求证:平面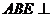 平面
平面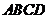 ;
;
(Ⅱ)若以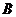 、
、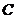 、
、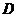 、
、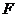 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为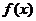 ,求
,求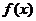 的最大值;
的最大值;
(Ⅲ)当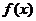 取得最大值时,求异面直线
取得最大值时,求异面直线 和
和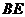 所成角的余弦值.
所成角的余弦值.
17.(本小题满分12分)
已知函数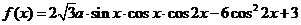 ,且
,且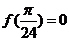 。
。
(Ⅰ)求函数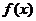 的周期
的周期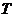 和单调递增区间;
和单调递增区间;
(Ⅱ)若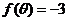 ,且
,且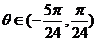 ,求
,求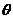 的值。
的值。
16.观察下表:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…………
则第__________行的各数之和等于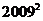 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com