
题目列表(包括答案和解析)
20.解:(1)由条件得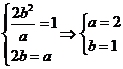 ,所以方程
,所以方程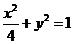 ………3分
………3分
(2)易知直线l斜率存在,令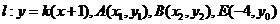
由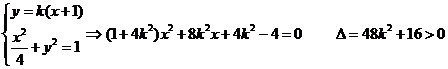
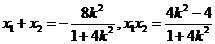 …………………6分
…………………6分
由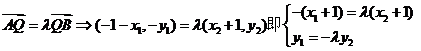
得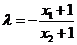 …………………8分
…………………8分
由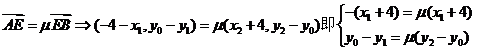
得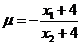 …………………10分
…………………10分
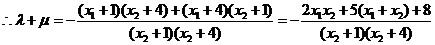
将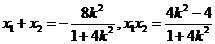 代入
代入
有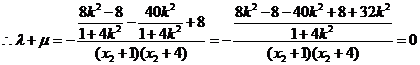 ……………12分
……………12分
22.(1)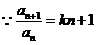 ,
,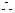
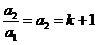 ………………………………….1分
………………………………….1分
又因为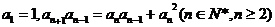 ,则
,则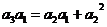 ,即
,即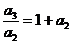 ,又
,又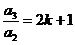 ,
,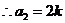 ,
,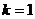 …………………………………….4分
…………………………………….4分
(2)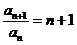 ,
,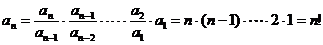 …….5分
…….5分
因为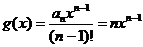 ,所以
,所以
当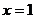 时,
时,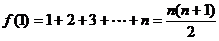
当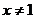 时,
时,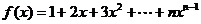 ,①
,①
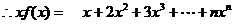 ,②
,②
①-②: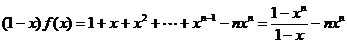 ,……………8分
,……………8分
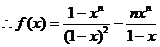 .综上所述,
.综上所述,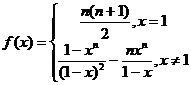 ……………9分
……………9分
(3)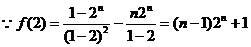 ,…………………………………..10分
,…………………………………..10分
又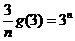 ,易验证当
,易验证当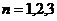 时不等式成立;…………………………………11分
时不等式成立;…………………………………11分
假设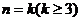 ,不等式成立,即
,不等式成立,即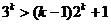 ,两边乘以3得
,两边乘以3得
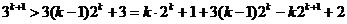
又因为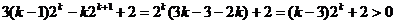
所以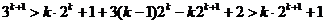
即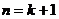 时不等式成立.故不等式恒成立……………………………………………..14分
时不等式成立.故不等式恒成立……………………………………………..14分
21.(1)由题设得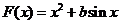 ,
,
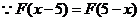 ,则
,则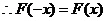 ,
,
所以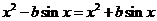 ……………………………………………………2分
……………………………………………………2分
所以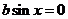 对于任意实数
对于任意实数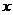 恒成立
恒成立
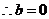 .故
.故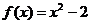 …………………………………………………………..3分
…………………………………………………………..3分
(2)由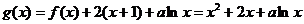 ,求导数得
,求导数得
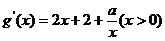 ,
,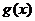 在
在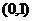 上恒单调,只需
上恒单调,只需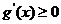 或
或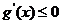 在
在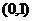 上恒成立,即
上恒成立,即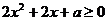 或
或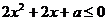 恒成立,所以
恒成立,所以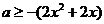 或
或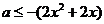 在
在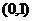 上恒成立…………………………………………………6分
上恒成立…………………………………………………6分
记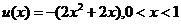 ,可知:
,可知: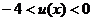 ,
,
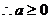 或
或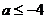 ………………………………………………………………….8分
………………………………………………………………….8分
(3)令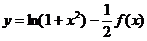 ,则
,则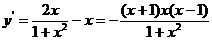 . 令
. 令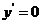 ,则
,则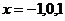 ,列表如下.
,列表如下.
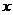 |
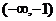 |
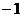 |
 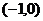 |
0 |
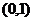 |
1 |
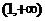 |
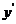 |
+ |
0 |
- |
0 |
+ |
0 |
- |
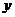 |
递增 |
极大值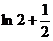 |
递减 |
极小值1 |
递增 |
极大值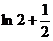 |
递减 |
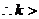
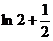 时,无零点;
时,无零点;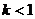 或
或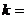
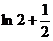 时,有两个零点;
时,有两个零点;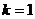 时有三个零点;
时有三个零点;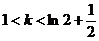 时,有四个零点…………………………………………………………12分
时,有四个零点…………………………………………………………12分
20.解:(1)由条件得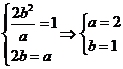 ,所以方程
,所以方程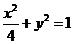 ………3分
………3分
(2)易知直线l斜率存在,令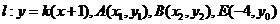
由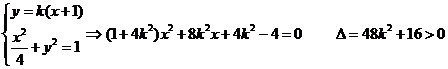
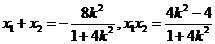 …………………6分
…………………6分
由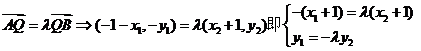
得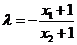 …………………8分
…………………8分
由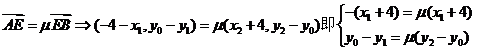
得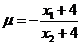 …………………10分
…………………10分
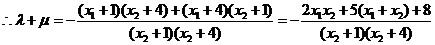
将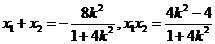 代入
代入
有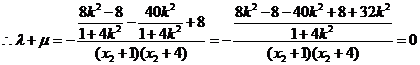 ……………12分
……………12分
19. (Ⅰ)由三视图可知: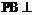 底面
底面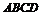 ,底面ABCD为直角梯形,PB=BC=CD=1,AB=2,∴
,底面ABCD为直角梯形,PB=BC=CD=1,AB=2,∴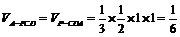 . …………3分
. …………3分
(Ⅱ)当M为PB的中点时,CM∥平面PDA. 取PA中点N,连结MN,DN,可证MN∥CD,且MN=CD,∴CM∥DN,故CM∥平面PDA. …………6分
(Ⅲ)分别以BC,BA,BP所在直线为x轴,y轴,z轴,建立空间直角坐标系. 则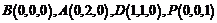 . 假设在BC边上存在点Q,使得二面角A-PD-Q为
. 假设在BC边上存在点Q,使得二面角A-PD-Q为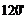 ,设
,设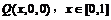 ,平面
,平面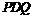 的法向量为
的法向量为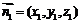 ,则由
,则由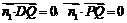 ,及
,及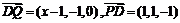 ,得
,得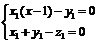 ,
,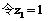 ,得
,得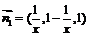 .
.
同理,设平面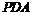 的法向量为
的法向量为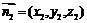 ,可得
,可得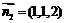 ;∴
;∴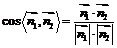
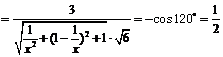 ,解得
,解得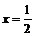 ,∴
,∴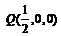 ,故存在点Q为BC的中点,使二面角A-PD-Q为
,故存在点Q为BC的中点,使二面角A-PD-Q为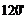 .………12分
.………12分
18.解:(Ⅰ)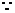 当
当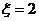 时,有
时,有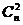 种坐法,
…………………………2分
种坐法,
…………………………2分
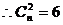 ,即
,即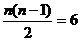 ,
,
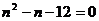 ,
,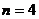 或
或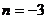 (舍去).
(舍去).
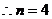 . ……………………4分
. ……………………4分
(Ⅱ)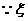 的可能取值是
的可能取值是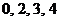 ,
,
又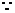
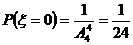 ,
, 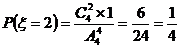 ,
,
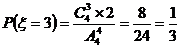 ,
,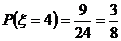 ,………………………8分
,………………………8分
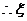 的概率分布列为:
的概率分布列为:
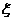 |
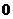 |
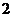 |
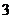 |
 |
|
P |
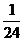 |
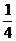 |
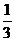 |
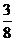 |
…………………10分
则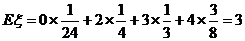 .
……………………12分
.
……………………12分
17.(1)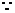
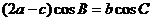 ,
,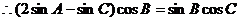 ,
,
即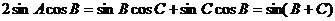 ……………………..3分
……………………..3分
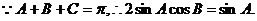
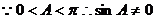 .
. 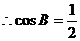 .
.
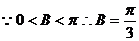 …………………………………………………………….6分
…………………………………………………………….6分
(2)m·n=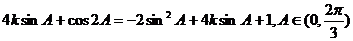 ,…..8分
,…..8分
设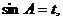 则
则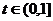 .
.
则m·n=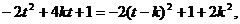
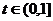 ……………………….10分
……………………….10分
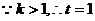 时,m·n取最大值.
时,m·n取最大值.
依题意得,(m·n) =
=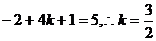 …………………………………12分
…………………………………12分
22.(本小题满分14分)
已知数列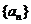 中,
中,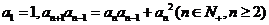 ,且
,且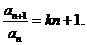 (1)求证:
(1)求证: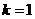 ;
(2)设
;
(2)设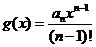 ,
,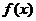 是数列
是数列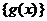 的前
的前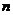 项和,求
项和,求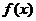 的解析式;
(3)求证:不等式
的解析式;
(3)求证:不等式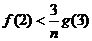 对于
对于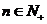 恒成立。
恒成立。
高三数学理科适应性训练试题答案及评分标准
21.(本小题满分12分)
已知函数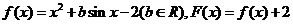 ,且对于任意实数
,且对于任意实数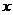 ,恒有
,恒有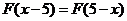 。
(1)求函数
。
(1)求函数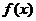 的解析式;
(2)已知函数
的解析式;
(2)已知函数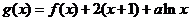 在区间
在区间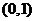 上单调,求实数
上单调,求实数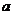 的取值范围;
(3)函数
的取值范围;
(3)函数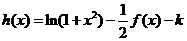 有几个零点?
有几个零点?
19.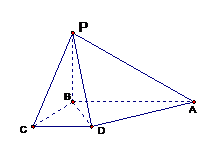 (本小题满分12分)
一个四棱锥的直观图和三视图如图所示:
(本小题满分12分)
一个四棱锥的直观图和三视图如图所示: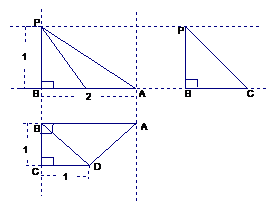
(Ⅰ)求三棱锥A-PDC的体积;
(Ⅱ)试在PB上求点M,使得CM∥平面PDA;
(Ⅲ) 在BC边上是否存在点Q,使得二面角A-PD-Q为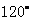 ?若存在,确定点Q的位置;若不存在,请说明理由.
?若存在,确定点Q的位置;若不存在,请说明理由.
20(本小题满分12分)
已知椭圆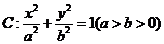 ,过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,点Q分
,过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,点Q分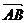 所成比为λ,点E分
所成比为λ,点E分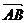 所成比为μ,求证λ+μ为定值,并计算出该定值.
所成比为μ,求证λ+μ为定值,并计算出该定值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com