
题目列表(包括答案和解析)
4.直线x-y+a=0被圆x2+y2=25所截得的弦长为8,则a =
3.棱长均为a的正四棱锥的体积为
2.函数f (x) =x2-x+的定义域和值域都是[1,a],(a>1),则a的取值是
1.若是纯虚数,则实数a=
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知:双曲线 方程为:
方程为: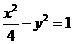 ,双曲线
,双曲线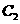 方程为:
方程为: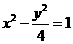
(1)分别求出它们的焦点坐标和渐近线方程;
(2)如图所示,过点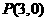 作斜率为3的直线分别与
作斜率为3的直线分别与
双曲线 和双曲线
和双曲线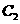 的右支相交。试判断线段
的右支相交。试判断线段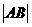 与
与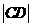 是否相等,并说明理由;
是否相等,并说明理由;
(3)过点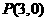 作直线
作直线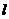 与双曲线
与双曲线 的右支和双曲线
的右支和双曲线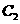 的右支相交,求直线
的右支相交,求直线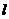 与双曲线
与双曲线 右支和双曲线
右支和双曲线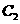 右支交点的总个数,并简要说明理由。
右支交点的总个数,并简要说明理由。
20.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已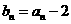 (
(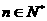 )知数列
)知数列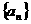 的首项
的首项 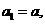
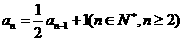 ,若
,若
(1)问数列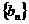 是否构成等比数列,并说明理由;
是否构成等比数列,并说明理由;
(2)若已知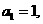 设无穷数列
设无穷数列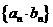 的各项和为
的各项和为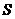 ,求
,求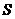
(3)在(2)的条件下,设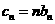 (
(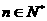 ),求数列
),求数列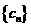 的最小值
的最小值
19.(本题满分14分) 本题共有2个小题,第1小题满分4分,第2小题满分10分.
若函数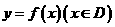 同时满足以下条件:
同时满足以下条件:
①它在定义域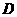 上是单调函数;
上是单调函数;
②存在区间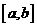
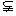
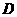 使得
使得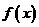 在
在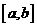 上的值域也是
上的值域也是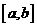 ,我们将这样的函数称作“
,我们将这样的函数称作“ 类函数”。
类函数”。
(1)函数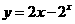 是不是“
是不是“ 类函数”?如果是,试找出
类函数”?如果是,试找出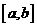 ;如果不是,试说明理由;
;如果不是,试说明理由;
(2)求使得函数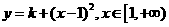 是“
是“ 类函数”的常数
类函数”的常数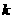 的取值范围。
的取值范围。
18.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
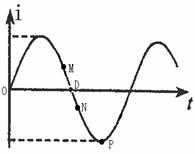
如图所示为电流强度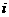 (安培)随时间
(安培)随时间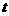 (秒)变化的关系式是:
(秒)变化的关系式是: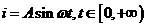 (其中
(其中 >0)的图象。若点
>0)的图象。若点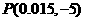 是图象上一最低点
是图象上一最低点
(1)求 ,
, ;
;
(2)已知点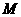 、点
、点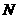 在图象上,点
在图象上,点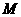 的坐标为
的坐标为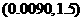 ,若点
,若点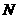 的坐标为
的坐标为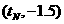 ,试用两种方法求出
,试用两种方法求出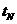 的值。(精确到0.0001秒)
的值。(精确到0.0001秒)
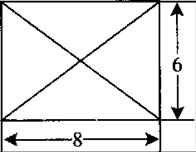
17.(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知某几何体的俯视图是如图5所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S
 [解:]
[解:]
16.下列条件中,不能确定A、B、C三点共线的是 ( )
A.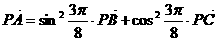 B.
B.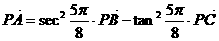
C.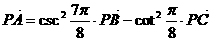 D.
D.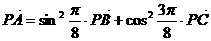
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com