
题目列表(包括答案和解析)
1.集合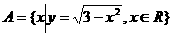 ,
,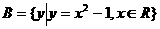 ,则
,则 =
=
A.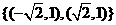 B.
B.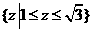
C.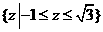 D.
D.
21.(14分)在数列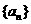 中,
中,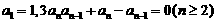
(Ⅰ)求数列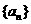 的通项;
的通项;
(Ⅱ)若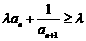 对任意
对任意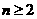 的整数恒成立,求实数
的整数恒成立,求实数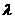 的取值范围;
的取值范围;
(Ⅲ)设数列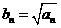 ,
,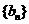 的前
的前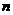 项和为
项和为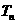 ,求证:
,求证: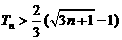 .
.
20.(14分)已知常数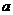 、
、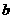 、
、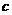 都是实数,函数
都是实数,函数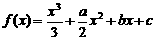 的导函数为
的导函数为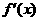
(Ⅰ)设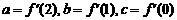 ,求函数f(x)的解析式;
,求函数f(x)的解析式;
(Ⅱ)设 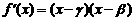 ,且
,且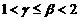 ,
,
①求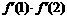 的取值范围;
的取值范围;
②问:是否存在正整数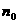 ,使得
,使得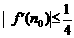 ?请说明理由.
?请说明理由.
19.(14分)已知圆O: 交
交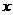 轴于A,B两点,曲线C是以AB为长轴,离心率为
轴于A,B两点,曲线C是以AB为长轴,离心率为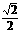 的椭圆,其左焦点为F,若P是圆O上一点,连结PF,过原点O作直线PF的垂线交直线x=-2于点Q.
的椭圆,其左焦点为F,若P是圆O上一点,连结PF,过原点O作直线PF的垂线交直线x=-2于点Q.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点P的坐标为(1,1),求证:直线PQ与圆O相切;
(Ⅲ)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关 系?若是,请证明;若不是,请说明理由.
系?若是,请证明;若不是,请说明理由.
18.(12分)如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
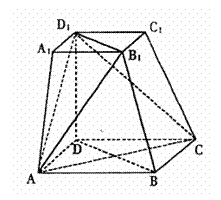 (Ⅰ)求证:B1B//平面D1AC;
(Ⅰ)求证:B1B//平面D1AC;
(Ⅱ)求二面角B1-AD1-C的余弦值.
17.(14分)某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定.他们三人都有“同
意”、“中立”、“反对”三类票各一张.投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为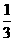 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
(Ⅰ)求此公司决定对该项目投资的概率;
(Ⅱ)记投票结果中“中立”票的张数为随机变量X,求X的分布列及数学期望EX.
16.(12分)已知向量 ,定义函数
,定义函数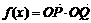 .
.
(Ⅰ)求函数f(x)的表达式,并指出其最大最小值;
(Ⅱ)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.
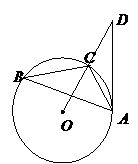
15.如图,已知:△ABC内接于圆O,点D在OC的延长线上,
AD是⊙O的切线,若∠B=300,AC=2,则OD的长为 .
14.若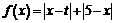 的最小值为3, 则实数t的值是______.
的最小值为3, 则实数t的值是______.
13. 极坐标系中,曲线
极坐标系中,曲线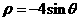 和
和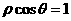 相交于点A,B,则
相交于点A,B,则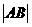 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com