
题目列表(包括答案和解析)
4. 数列
数列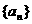 中,
中,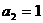 ,
,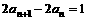 ,则
,则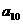 等于
等于
 A.
A.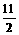 B.
B.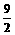 C.6
D.5
C.6
D.5
3.函数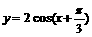 图象的一个对称中心是
图象的一个对称中心是
A.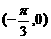 B.
B.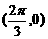 C.
C.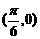 D.
D.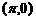
2.已知复数 是方程
是方程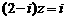 的解,且
的解,且 对应的向量
对应的向量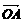 与向量
与向量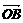 关于实轴对称,则向量
关于实轴对称,则向量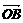 对应的复数为
对应的复数为
A.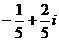 B.
B.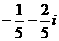 C.
C.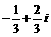 D.
D.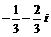
1.已知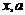 为实数,则“
为实数,则“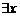 使
使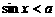 成立”是“
成立”是“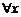 使
使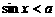 成立”的
成立”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不必要也不充分条件
21.解:(1)矩阵A的特征多项式为
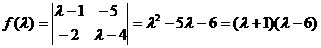 ……2分
……2分
令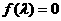 ,得矩阵A的特征值为
,得矩阵A的特征值为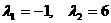 …………3分
…………3分
对于特征值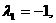 解相应的线性方程组
解相应的线性方程组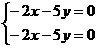 得一个非零解
得一个非零解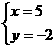 ,
,
因此,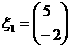 是矩阵A的属于特征值
是矩阵A的属于特征值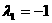 的一个特征向量。……5分
的一个特征向量。……5分
对于特征值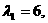 解相应的线性方程组
解相应的线性方程组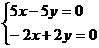 得一个非零解
得一个非零解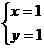 ,
,
因此,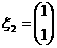 是矩阵A的属于特征值
是矩阵A的属于特征值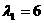 的一个特征向量。………7分
的一个特征向量。………7分
(2)点P的轨迹是上半圆: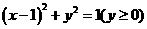 ………2分
………2分
点P的轨迹是直线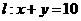 ………4分
所以
………4分
所以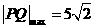 ………7分
………7分
(3)设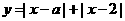 ,则
,则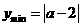 ………3分
………3分
因为不等式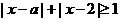 对
对 恒成立………5分
恒成立………5分
所以 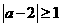 ,解得:
,解得: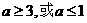 ………7分
………7分
本资料由《七彩教育网》 提供!
20.(本题满分14分)
解:(Ⅰ)由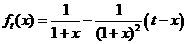 ,得
,得
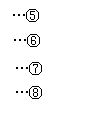 则
则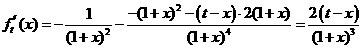 ………2分
………2分
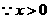 ,∴当
,∴当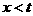 时,
时,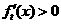 ;当
;当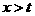 时,
时,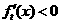 ,
,
∴当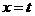 时,
时,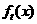 取得最大值
取得最大值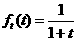 .…………4分
.…………4分
(Ⅱ)由题意知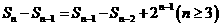 ,即
,即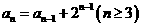 …5分
…5分
∴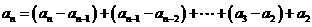
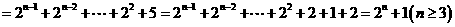 ……6分
……6分
检验知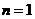 、
、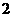 时,结论也成立,故
时,结论也成立,故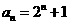 .…………7分
.…………7分
所以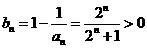 ,令
,令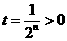 ,则
,则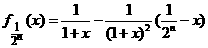 ,
,
由(Ⅰ)可知, 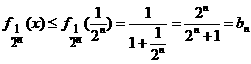 .
.
∴对任意的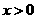 ,不等式
,不等式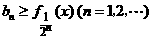 成立. ………9分
成立. ………9分
(Ⅲ)由(Ⅱ)知,对任意的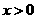 ,有
,有
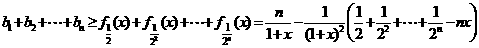 .…10分
.…10分
令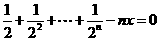 ,则
,则
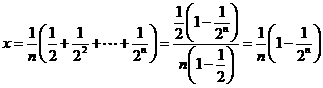 ……12分
……12分
则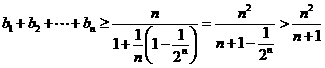 . ∴原不等式成立.…14分
. ∴原不等式成立.…14分
19.解:(I)设所求椭圆是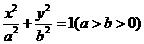 (1分)
由题意得
(1分)
由题意得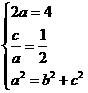 3分
3分
解得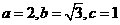 (5分) 所以椭圆方程为
(5分) 所以椭圆方程为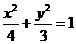 (5分)
(5分)
(Ⅱ)直线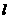 方程为
方程为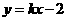 ,则
,则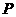 的坐标为
的坐标为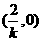 (6分)
(6分)
设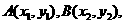 则
则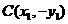 ,
,
直线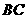 方程为
方程为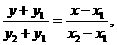 令
令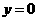 ,得
,得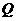 的横坐标为
的横坐标为
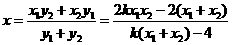 ① (8分)
① (8分)
又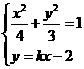 得
得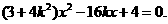 得
得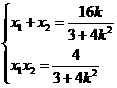 ,(9分)
,(9分)
代入①得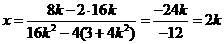 , (11分)
, (11分)
得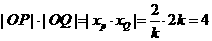 ,
, 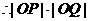 为常数4 (13分)
为常数4 (13分)
18.(本题满分14分)
解:(Ⅰ)频率分布直方图如右图所示.……4分
(Ⅱ)睡眠时间小于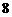 小时的概率是
小时的概率是
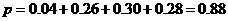 . ………8分
. ………8分
(Ⅲ)首先要理解直到型循环结构图的含义,输入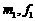 的值后,
的值后,
由赋值语句: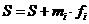 可知,流程图进入一个求和状态.
可知,流程图进入一个求和状态.
令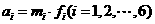 ,数列
,数列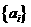 的前
的前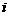 项和为
项和为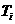 ,即:
,即:
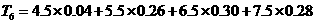
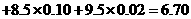 -11分
-11分
则输出的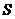 为
为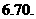
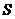 的统计意义即是指参加调查者的平均睡眠时间,
的统计意义即是指参加调查者的平均睡眠时间,
从统计量的角度来看,即是睡眠时间的期望值. ……………13分
17.解:(1)∵四边形DCBE为平行四边形 ∴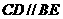
∵ DC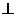 平面ABC
∴
平面ABC
∴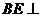 平面ABC
平面ABC
∴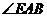 为AE与平面ABC所成的角,即
为AE与平面ABC所成的角,即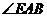 =
=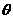 ------1分
------1分
 在Rt△ABE中,由
在Rt△ABE中,由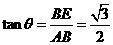 ,
,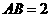 得
得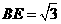 ------------2分
------------2分
∵AB是圆O的直径 ∴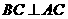 ∴
∴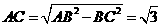
∴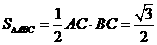 ----3分
----3分
∴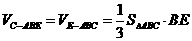
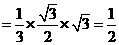 ------4分
------4分
(2)证明:∵ DC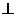 平面ABC ,
平面ABC ,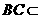 平面ABC ∴
平面ABC ∴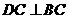 . --------5分
. --------5分
∵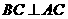 且
且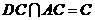 ∴
∴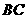
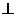 平面ADC.
平面ADC.
∵DE//BC ∴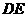
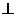 平面ADC ----------7分
平面ADC ----------7分
又∵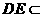 平面ADE ∴平面ACD
平面ADE ∴平面ACD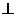 平面
平面 -------8分
-------8分
(3)在CD上存在点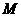 ,使得MO
,使得MO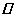 平面
平面 ,该点
,该点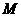 为
为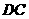 的中点.-----9分
的中点.-----9分
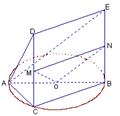
证明如下: 如图,取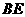 的中点
的中点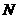 ,连MO、MN、NO,∵M、N、O分别为CD、BE、AB的中点, ∴MN//DE. --------10分
,连MO、MN、NO,∵M、N、O分别为CD、BE、AB的中点, ∴MN//DE. --------10分
∵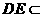 平面ADE,
平面ADE,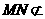 平面ADE,∴MN//平面ADE --------------11分
平面ADE,∴MN//平面ADE --------------11分
同理可得NO//平面ADE.∵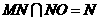 ,∴平面MNO//平面ADE. -----12分
,∴平面MNO//平面ADE. -----12分
∵ 平面MNO,∴
平面MNO,∴ ∥平面ADE. ------13分(其它证法请参照给分)
∥平面ADE. ------13分(其它证法请参照给分)
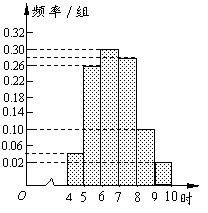
16.解:(1)由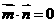 得
得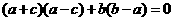
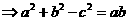 ---2分
---2分
由余弦定理得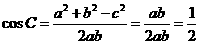 ---4分
---4分
∵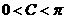 ∴
∴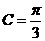 ----6分
----6分
(2)∵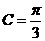 ∴
∴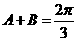
∴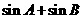 =
=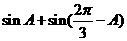
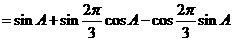
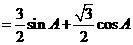
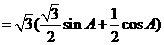
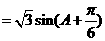 ---------9分
---------9分
∵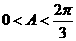 ∴
∴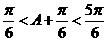 ∴
∴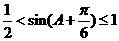 ∴
∴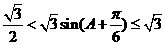
即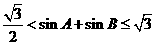 .----------13分
.----------13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com