
题目列表(包括答案和解析)
18.(本小题满分12分)
解:(Ⅰ)设抛掷一次这样的硬币,正面朝上的概率为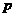 ,
,
依题意有: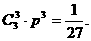 ∴
∴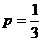
所以,抛掷这样的硬币三次,恰有两次正面朝上的概率为
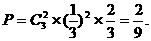 …………………………6分
…………………………6分
(Ⅱ)解:四次抛掷后正面朝上的总次数 的可能取值为0,1,2,
的可能取值为0,1,2,
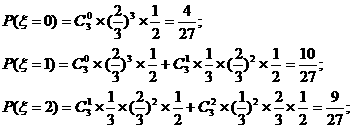
……………………9分
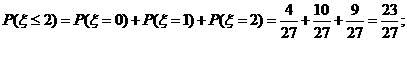
所以,四次抛掷后正面朝上的总次数至多两次的概率为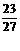 。…………………12分
。…………………12分
17.(本小题满分12分)
方法一:(Ⅰ)证明:在△PBC中,BC=PC=1,PB=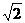 ,
,
∴BC2+PC2=PB2,
∴∠PCB=90°,即PC⊥BC, ……………… 1分
∵AB⊥PC,AB∩BC=B,
∴PC⊥平面ABCD. ………………4分
(Ⅱ)如图,连接AC,由(Ⅰ)知PC⊥平面ABCD,
∴AC为PA在平面ABCD内的射影,
∴∠PAC为PA与平面ABCD所成的角. ……………… 6分
在△ABC中,∠ABC=90°,AB=BC=1,
∴AC=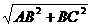 =
=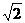 , 在△PAC中,∠PCA=90°,PC=1,AC=
, 在△PAC中,∠PCA=90°,PC=1,AC=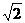 ,
,
∴tan∠PAC=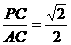 ,
,
∴PA与平面ABCD所成角的大小为arctan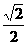 . ……………… 8分
. ……………… 8分
(Ⅲ)由(Ⅰ)知PC⊥BC, 又BC⊥CD,PC∩CD=C,
∴BC⊥平面PCD. ………………9分
如图,过C作CM⊥PD于M连接BM,
∴CM是BM在平面PCD内的射影, ∴BM⊥PD,
∴∠CMB为二面角B-PD-C的平面角. ………………10分
在△PCD中,∠PCD=90°,PC=1,CD=2,
∴PD=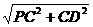 =
=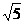 , 又CM⊥PD,
, 又CM⊥PD,
∴PD·CM=PC·CD, ∴CM=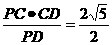
在△CMB中,∠BCM=90°,BC=1,CM=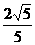 , ∴tan∠CMB=
, ∴tan∠CMB=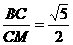 ,
,
∴二面角B-PD-C的大小为 arctan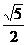 .
……………… 12分
.
……………… 12分
方法二:(Ⅰ)同方法一. ……………… 4分
(Ⅱ)解:连接AC,由(Ⅰ)知PC⊥平面ABCD,
∴AC为PA在平面ABCD内的射影,
∴∠PAC为PA与平面ABCD所成的角. ………………6分
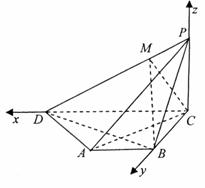
如图,在平面ABCD内,以C为原点,CD、CB、CP分别为x、y,z轴,建立空间直角坐标系C-xyz,
则C(0,0,0),B(0,1,0),D(2,0,0),P(0,0,1),A(1,1,0),
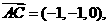
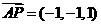 ………………7分
………………7分
∴cos∠PAC =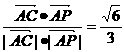 ,
,
∴PA与平面ABCD所成角的大小为arccos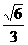 . ………………8分
. ………………8分
(Ⅲ)过C作CM⊥DP于M,连接BM,设M(x,y,z),
则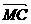 =(-x,-y,-z),
=(-x,-y,-z),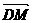 =(x-2,y,z),
=(x-2,y,z),
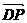 =(-2,0,1),
=(-2,0,1),
∴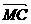 ⊥
⊥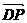 , ∴
, ∴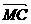 ·
·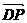 =2x-z=0;
①
=2x-z=0;
①
∵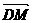 ,
,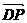 共线,∴y=0,
共线,∴y=0,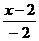 =z, ②
=z, ②
由①②,解得x=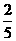 ,y=0,z=
,y=0,z=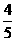 ,
,
∴M点的坐标为(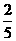 ,0,
,0,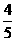 ),
),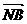 =(-
=(-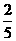 ,1,-
,1,-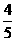 ),
),
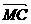 =(-
=(-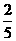 ,0,-
,0,-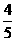 ) ………………9分
) ………………9分
∵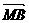 ·
·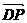 =
=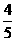 +0-
+0-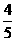 =0,
=0,
∴MB⊥DP, 又CM⊥DP,
∴∠CMB为二面角B-PD-C的平面角. ……………… 10分
∵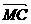 =(-
=(-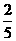 ,0,-
,0,-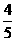 ),
),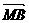 =(-
=(-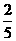 ,1,-
,1,-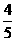 )
)
∴cos∠CMB=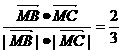 ,
,
∴二面角B-PD-C的大小为arccos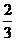 .
………………12分
.
………………12分
16.(本小题满分12分)
解:(I)因为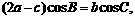
所以 ………………2分
………………2分
整理得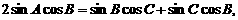
所以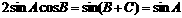 ,
………………4分
,
………………4分
因为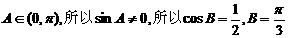 .……………………6分
.……………………6分
(Ⅱ)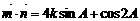 ……………………7分
……………………7分
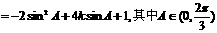 ……………………8分
……………………8分
设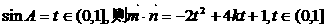 , 又k>1
, 又k>1
所以,当 取得最大值.
……………………9分
取得最大值.
……………………9分
依题意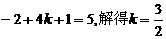 ,符合题意. 所以,
,符合题意. 所以,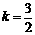 . ………12分
. ………12分
14. 18 15. 5; 2
11. 36
12. 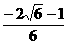 13. 60
13. 60
21.(本小题满分14分)
已知函数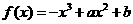 (a,b∈R).
(a,b∈R).
(Ⅰ)若a=1,函数f(x)的图象能否总在直线y=b的下方?说明理由;
(Ⅱ)若函数f(x)在(0,2)上是增函数,求a的取值范围;
(Ⅲ)设x1,x2,x3为方程f(x)=0的三个根,且x1∈(-1,0),x2∈(0,1),
x3∈(-∞,-1)∪(1,+∞) . 求证:│a│>1.
夷陵中学2009届高考适应性测试
数 学 试 题 (文科)
20.(本小题满分13分)
已知椭圆C:x2+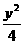 =1,过点M(0,1)的直线l与椭圆C相交于两点A、B.
=1,过点M(0,1)的直线l与椭圆C相交于两点A、B.
(Ⅰ)若l与x轴相交于点P,且P为AM的中点,求直线l的方程;
(Ⅱ)设点N(0,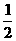 ),求│
),求│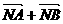 │的最大值.
│的最大值.
19.(本小题满分12分)
设等差数列{an}的前n项和为Sn,且Sn=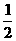 nan+an-c(c是常数,n∈N*),a2=6.
nan+an-c(c是常数,n∈N*),a2=6.
(Ⅰ)求c的值及{an}的通项公式;
(Ⅱ)证明: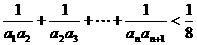 .
.
18.(本小题满分12分)已知将一枚质地不均匀的硬币抛掷三次,三次正面均朝上的概率为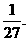
(Ⅰ)求抛掷这样的硬币三次,恰有两次正面朝上的概率;
(Ⅱ)抛掷这样的硬币三次后,再抛掷一枚质地均匀的硬币一次,求四次抛掷后正面朝上的总次数至多两次的概率。
17.(本小题满分12分)
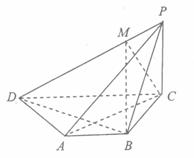
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BCD=90°,
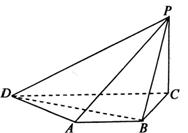 AB∥CD,又AB=BC=PC=1,PB=
AB∥CD,又AB=BC=PC=1,PB=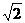 , CD=2,AB⊥PC.
, CD=2,AB⊥PC.
(Ⅰ)求证:PC⊥平面ABCD;
(Ⅱ)求PA与平面ABCD所成角的大小;
(Ⅲ)求二面角B-PD-C的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com