
题目列表(包括答案和解析)
[题9]已知数列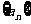 满足
满足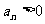 ,且对一切
,且对一切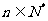 ,有
,有 ,其中
,其中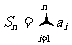 .
.
(1)求证:对一切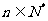 ,有
,有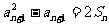 ;
;
(2)求数列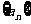 的通项公式;
的通项公式;
(3)求证: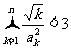 .
.
[题10]已知函数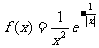 (
(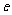 为自然对数的底数),
为自然对数的底数),
(1)判断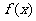 的奇偶性;
的奇偶性;
(2)在 上求函数的极值;
上求函数的极值;
(3)用数学归纳法证明:当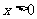 时,对任意正整数
时,对任意正整数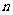 都有
都有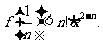
[题11]已知函数
(1)求函数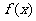 的单调区间;
的单调区间;
(2)如果关于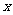 的方程
的方程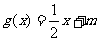 有实数根,求实数
有实数根,求实数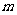 的取值集合;
的取值集合;
(3)是否存在正数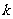 ,使得关于
,使得关于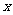 的方程
的方程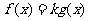 有两个不相等的实数根?如果存在,求
有两个不相等的实数根?如果存在,求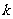 满足的条件;如果不存在,说明理由.
满足的条件;如果不存在,说明理由.
例8.2008全国卷II-18(本小题满分12分)购买某种保险,每个投保人每年度向保险公司交纳保费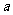 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为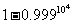 .
.
(Ⅰ)求一投保人在一年度内出险的概率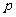 ;
;
(Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50 000元,为保证盈利的期望不小于0,求每位投保人应交纳的最低保费(单位:元).
不急不燥、冷静思考、沉着应答是解出问题的关键。相信它不会比平时综合训练试题难多少,也许是情景新一点、条件隐晦一点、设问巧一点,没有什么大不了的,我不求超水平发挥,只求正常发挥自己的水平,做出该做得起的题即可。“战略上要藐视它,战术上要重视它”。
高考数学题中,最后三个大题往往是综合的知识多、技巧性强、能力要求高的综合性题目,它解答成功与否将直接影响着升学档次。大量未成功的考生并不完全是水平和能力问题,而是心理不佳、方法不当,导致宝贵的时间白白流失,发挥不出自己应有的水平,使自己无缘问鼎名校或重点大学,饮恨终身。那么面对综合试题,考生应答呢?
1. 下表给出一个“等差数阵”:
|
4 |
7 |
( ) |
( ) |
( ) |
…… |
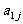 |
…… |
|
7 |
12 |
( ) |
( ) |
( ) |
…… |
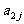 |
…… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
…… |
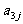 |
…… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
…… |
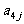 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
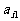 |
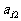 |
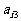 |
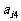 |
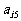 |
…… |
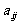 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
其中每行、每列都是等差数列,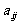 表示位于第i行第j列的数.(1)写出
表示位于第i行第j列的数.(1)写出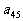 的值; (2)写出
的值; (2)写出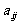 的计算公式;(3)证明:正整数N在该等差数列阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
的计算公式;(3)证明:正整数N在该等差数列阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
4.在x0y平面上给定曲线y2=2x, 设点A坐标为(a,0), aÎR,求曲线上点到点A距离的最小值d,并写成d=f(a)的函数表达式.
3.已知关于x的不等式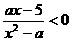 的解集为M.
的解集为M.
(1)当a=4时,求集合M:
(2)若3ÎM,求实数a的取值范围.
2.解不等式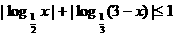
1.解不等式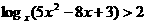
2.能够合理,正确地求解有关问题
命题分析:
分类讨论是一种重要的逻辑方法,也是一种常用的数学方法,这可以培养学生思维的条理性和概括性,以及认识问题的全面性和深刻性,提高学生分析问题,解决问题的能力.因此分类讨论是历年数学高考的重点与热点.而且也是高考的一个难点.这次的一模考试中,尤其是西城与海淀都设置了解答题来考察学生对分类讨论问题的掌握情况.
重点题型分析:
例1.解关于x的不等式: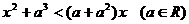
解:原不等式可分解因式为:(x-a)(x-a2)<0
(下面按两个根的大小关系分类)
(1)当a>a2Þa2-a<0即 0<a<1时,不等式的解为 xÎ(a2, a).
(2)当a<a2Þa2-a>0即a<0或a>1时,不等式的解为:xÎ(a, a2)
(3)当a=a2Þa2-a=0 即 a=0或 a=1时,不等式为x2<0或(x-1)2<0
不等式的解为 xÎÆ.
综上,当 0<a<1时,xÎ(a2, a)
当a<0或a>1时,xÎ(a,a2)
当a=0或a=1时,xÎÆ.
评述:抓住分类的转折点,此题分解因式后,之所以不能马上写出解集,主要是不知两根谁大谁小,那么就按两个根之间的大小关系来分类.
例2.解关于x的不等式 ax2+2ax+1>0(aÎR)
解:此题应按a是否为0来分类.
(1)当a=0时,不等式为1>0, 解集为R.
(2)a¹0时分为a>0 与a<0两类
①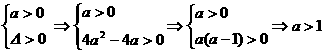 时,方程ax2+2ax+1=0有两根
时,方程ax2+2ax+1=0有两根
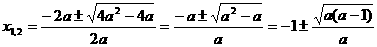 .
.
则原不等式的解为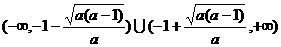 .
.
②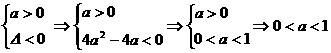 时,
时,
方程ax2+2ax+1=0没有实根,此时为开口向上的抛物线,则不等式的解为(-¥,+¥).
③ 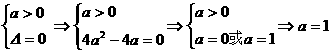 时,
时,
方程ax2+2ax+1=0只有一根为x=-1,则原不等式的解为(-¥,-1)∪(-1,+¥).
④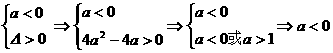 时,
时,
方程ax2+2ax+1=0有两根,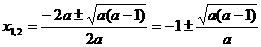
此时,抛物线的开口向下的抛物线,故原不等式的解为:
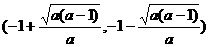 .
.
⑤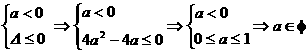
综上:
当0≤a<1时,解集为(-¥,+¥).
当a>1时,解集为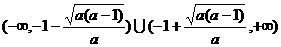 .
.
当a=1时,解集为(-¥,-1)∪(-1,+¥).
当a<0时,解集为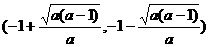 .
.
例3.解关于x的不等式ax2-2≥2x-ax(a∈R)(西城2003’一模 理科)
解:原不等式可化为Û ax2+(a-2)x-2≥0,
(1)a=0时,x≤-1,即x∈(-∞,-1].
(2)a¹0时,不等式即为(ax-2)(x+1)≥0.
① a>0时, 不等式化为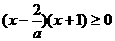 ,
,
当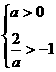 ,即a>0时,不等式解为
,即a>0时,不等式解为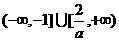 .
.
当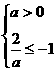 ,此时a不存在.
,此时a不存在.
② a<0时,不等式化为 ,
,
当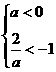 ,即-2<a<0时,不等式解为
,即-2<a<0时,不等式解为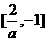
当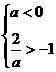 ,即a<-2时,不等式解为
,即a<-2时,不等式解为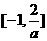 .
.
当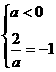 ,即a=-2时,不等式解为x=-1.
,即a=-2时,不等式解为x=-1.
综上:
a=0时,x∈(-∞,-1).
a>0时,x∈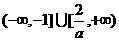 .
.
-2<a<0时,x∈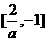 .
.
a<-2时,x∈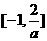 .
.
a=-2时,x∈{x|x=-1}.
评述:通过上面三个例题的分析与解答,可以概括出分类讨论问题的基本原则为:
10:能不分则不分;
20:若不分则无法确定任何一个结果;
30:若分的话,则按谁碍事就分谁.
例4.已知函数f(x)=cos2x+asinx-a2+2a+5.有最大值2,求实数a的取值.
解:f(x)=1-sin2x+asinx-a2+2a+5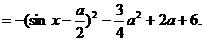
令sinx=t, t∈[-1,1].
则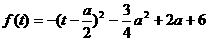 (t∈[-1,1]).
(t∈[-1,1]).
(1)当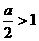 即a>2时,t=1,
即a>2时,t=1,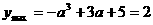
解方程得: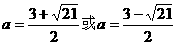 (舍).
(舍).
(2)当 时,即-2≤a≤2时,
时,即-2≤a≤2时,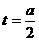 ,
,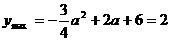 ,
,
解方程为: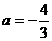 或a=4(舍).
或a=4(舍).
(3)当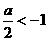 即a<-2时, t=-1时,ymax=-a2+a+5=2
即a<-2时, t=-1时,ymax=-a2+a+5=2
即 a2-a-3=0 ∴ 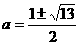 , ∵ a<-2, ∴
, ∵ a<-2, ∴ 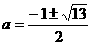 全都舍去.
全都舍去.
综上,当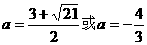 时,能使函数f(x)的最大值为2.
时,能使函数f(x)的最大值为2.
例5.设{an}是由正数组成的等比数列,Sn是其前n项和,证明: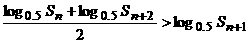 .
.
证明:(1)当q=1时,Sn=na1从而 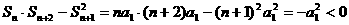
(2)当q≠1时,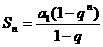 , 从而
, 从而
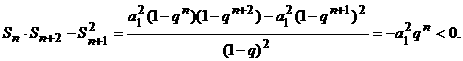
由(1)(2)得: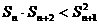 .
.
∵ 函数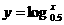 为单调递减函数.∴
为单调递减函数.∴ 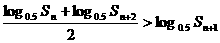 .
.
例6.设一双曲线的两条渐近线方程为2x-y+1=0, 2x+y-5=0,求此双曲线的离心率.
分析:由双曲线的渐近线方程,不能确定其焦点位置,所以应分两种情况求解.
解:(1)当双曲线的焦点在直线y=3时,双曲线的方程可改为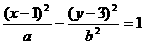 ,一条渐近线的斜率为
,一条渐近线的斜率为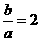 , ∴ b=2.∴
, ∴ b=2.∴ 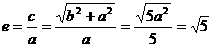 .
.
(2)当双曲线的焦点在直线x=1时,仿(1)知双曲线的一条渐近线的斜率为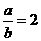 ,此时
,此时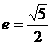 .
.
综上(1)(2)可知,双曲线的离心率等于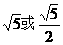 .
.
评述:例5,例6,的分类讨论是由公式的限制条件与图形的不确定性所引起的,而例1-4是对于含有参数的问题而对参数的允许值进行的全面讨论.
例7.解关于x的不等式 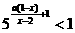 .
.
解:原不等式 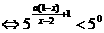
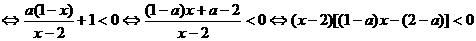
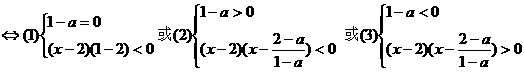
由(1) a=1时,x-2>0, 即 x∈(2,+∞).
由(2)a<1时,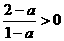 ,下面分为三种情况.
,下面分为三种情况.
①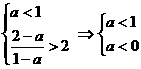 即a<1时,解为
即a<1时,解为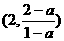 .
.
②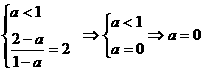 时,解为Æ.
时,解为Æ.
③ 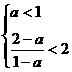 Þ
Þ 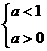 即0<a<1时,原不等式解为:
即0<a<1时,原不等式解为: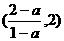 .
.
由(3)a>1时,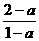 的符号不确定,也分为3种情况.
的符号不确定,也分为3种情况.
①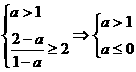 Þ a不存在.
Þ a不存在.
② 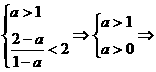 当a>1时,原不等式的解为:
当a>1时,原不等式的解为: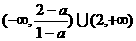 .
.
综上:
a=1时,x∈(2,+∞).
a<1时,x∈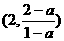
a=0时,xÎÆ.
0<a<1时,x∈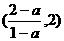
a>1时,x∈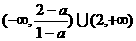 .
.
评述:对于分类讨论的解题程序可大致分为以下几个步骤:
10:明确讨论的对象,确定对象的全体;
20:确定分类标准,正确分类,不重不漏;
30:逐步进行讨论,获得结段性结记;
40:归纳总结,综合结记.
课后练习:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com