
题目列表(包括答案和解析)
2. 江西师大附中二模
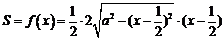
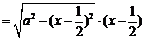
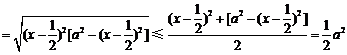 ,
,
等号成立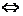
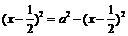
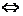
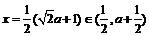 .
.
∴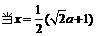 时,
时, .…………………………………………10分
.…………………………………………10分
A.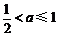 时,∵
时,∵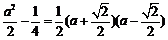 ,
,
∴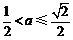 时.当
时.当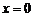 ,
,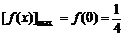 ,
,
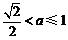 时,当
时,当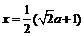 ,
, .……………………………12分
.……………………………12分
B.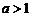 时,
时,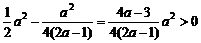 .
.
当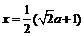 时,
时, .……………………………………………14分
.……………………………………………14分
综上,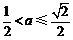 时,当
时,当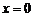 时,
时,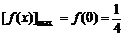 ,即MN与AB之间的距离为0米时,三角通风窗EMN的通风面积最大,最大面积为
,即MN与AB之间的距离为0米时,三角通风窗EMN的通风面积最大,最大面积为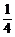 平方米.
平方米.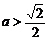 时,当
时,当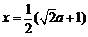 时,
时, ,
即
,
即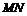 与
与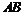 之间的距离为
之间的距离为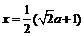 米时,三角通风窗EMN的通风面积最大,最大面积为
米时,三角通风窗EMN的通风面积最大,最大面积为 平方米.………………………16分
平方米.………………………16分
20.(本小题满分16分)
设函数f(x)=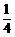 x4+bx2+cx+d,当x=t1时,f(x)有极小值.
x4+bx2+cx+d,当x=t1时,f(x)有极小值.
(1)若b=-6时,函数f(x)有极大值,求实数c的取值范围;
(2)在(1)的条件下,若存在实数c,使函数f(x)在闭区间[m-2,m+2]上单调递增,求实数m的取值范围;
(3)若函数f(x)只有一个极值点,且存在t2∈(t1,t1+1),使f ′(t2)=0,证明:函数g(x)=f(x)-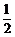 x2+t1x在区间(t1,t2)内最多有一个零点.
x2+t1x在区间(t1,t2)内最多有一个零点.
20解:(1)因为 f(x)=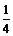 x4+bx2+cx+d,所以h(x)=f ′(x)=x3-12x+c.……2分
x4+bx2+cx+d,所以h(x)=f ′(x)=x3-12x+c.……2分
由题设,方程h(x)=0有三个互异的实根.
考察函数h(x)=x3-12x+c,则h ′(x)=0,得x=±2.
|
x |
(-∞,-2) |
-2 |
(-2,2) |
2 |
(2,+∞) |
|
h ′(x) |
+ |
0 |
- |
0 |
+ |
|
h(x) |
增 |
c+16 (极大值) |
减 |
c-16(
极小值) |
增 |
所以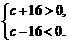 故-16<c<16. ………………………………………………5分
故-16<c<16. ………………………………………………5分
(2)存在c∈(-16,16),使f ′(x)≥0,即x3-12x≥-c, (*)
所以x3-12x>-16,
即(x-2)2(x+4)>0(*)在区间[m-2,m+2]上恒成立. …………7分
所以[m-2,m+2]是不等式(*)解集的子集.
所以 或m-2>2,即-2<m<0,或m>4. ………………………9分
或m-2>2,即-2<m<0,或m>4. ………………………9分
(3)由题设,可得存在α,β∈R,使
f ′(x)=x3+2bx+c=(x-t1)(x2+αx+β),
且x2+αx+β≥0恒成立. …………………………………………………11分
又f´(t2)=0,且在x=t2两侧同号,
所以f´(x) =(x-t1)(x-t2)2. …………………………………………13分
另一方面,
g ′(x)=x3+(2b-1)x+t1+c
=x3+2bx+c-(x-t1)=(x-t1)[(x-t2)2-1].
因为 t1 < x < t2,且 t2-t1<1,所以-1< t1-t2 < x-t2 <0.
所以 0<(x-t2)2<1,所以(x-t2)2-1<0.
而 x-t1>0,所以g ′(x)<0,所以g(x)在(t1,t2)内单调减.
从而g(x)在(t1,t2)内最多有一个零点.…………………………………16分
∴ ………………………………5分
………………………………5分
(2)
(一)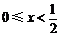 时,
时,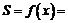
 .
.
∵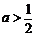 ,∴
,∴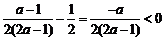 ,∴
,∴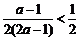 .
.
①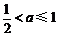 ,当
,当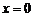 时,
时,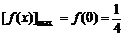 .
.
②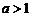 ,当
,当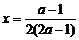 时,
时,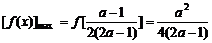 .……………7分
.……………7分
21. 解析:(Ⅰ)由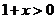 得函数
得函数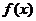 的定义域为
的定义域为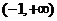 ,
,
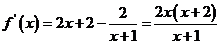 。
……………………………… 2分
。
……………………………… 2分
由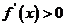 得
得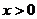 ;由
;由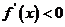 得
得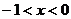 ,
,
∴函数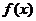 的递增区间是
的递增区间是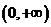 ;递减区间是
;递减区间是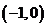 。……………………………… 4分
。……………………………… 4分
(Ⅱ)由(1)知,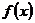 在
在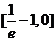 上递减,在
上递减,在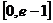 上递增。 ∴
上递增。 ∴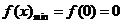
又∵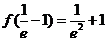 ,
,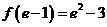 ,且
,且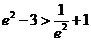 ,
,
∴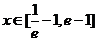 时,
时,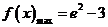 。
……………………………… 6分
。
……………………………… 6分
∵不等式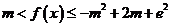 恒成立, ∴
恒成立, ∴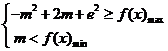 ,
,
即
∵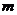 是整数,∴
是整数,∴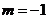 。
。
∴存在整数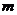 ,使不等式
,使不等式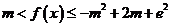 恒成立。 …………………… 9分
恒成立。 …………………… 9分
(Ⅲ)由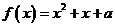 得
得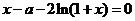 ,
,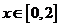
令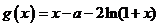 ,则
,则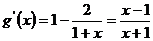 ,
,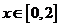
由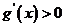 得
得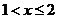 ;由
;由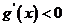 得
得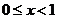 。
。
∴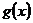 在
在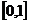 上单调递减,在
上单调递减,在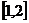 上单调递增. ……………………………… 11分
上单调递增. ……………………………… 11分
∵方程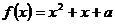 在
在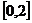 上恰有两个相异的实根,
上恰有两个相异的实根,
∴函数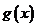 在
在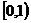 和
和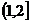 上各有一个零点,
上各有一个零点,
∴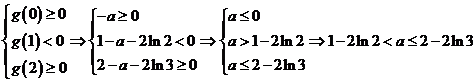 ,
,
∴实数 的取值范围是
的取值范围是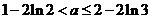 ………………………… 14分
………………………… 14分
21. (本小题满分14分)设函数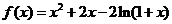 .(Ⅰ)求函数
.(Ⅰ)求函数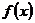 的单调区间;
的单调区间;
(Ⅱ)当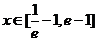 时,是否存在整数
时,是否存在整数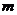 ,使不等式
,使不等式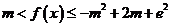 恒成立?若存在,求整数
恒成立?若存在,求整数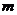 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(Ⅲ)关于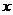 的方程
的方程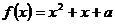 在
在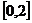 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数 的取值范围。
的取值范围。
20. 解析:(Ⅰ) ∵
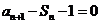 ①
①
∴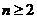 时,
时, 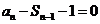 ②
②
①─②得: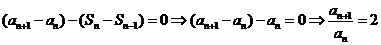
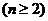 ……2分
……2分
由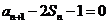 及
及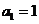 得
得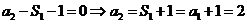
∴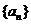 是首项为
是首项为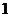 ,公比为2的等比数列,∴
,公比为2的等比数列,∴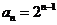 ……………… 4分
……………… 4分
(Ⅱ)解法一:由(Ⅰ)知 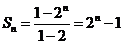 ……………… 5分
……………… 5分
若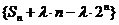 为等差数列,
为等差数列,
则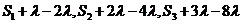 则成等差数列, …………………………… 6分
则成等差数列, …………………………… 6分
∴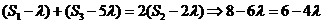 ,∴
,∴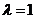 ………… 8分
………… 8分
当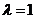 时,
时,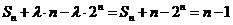 ,显然
,显然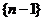 成等差数列,
成等差数列,
∴存在实数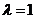 ,使得数列
,使得数列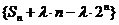 成等差数列。 ……………… 9分
成等差数列。 ……………… 9分
解法二:由(Ⅰ)知 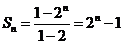 ……………… 5分
……………… 5分
∴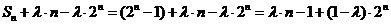 …………… 7分
…………… 7分
要使数列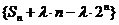 成等差数列,则只须
成等差数列,则只须 ,即
,即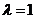 即可。……………8分
即可。……………8分
故存在实数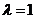 ,使得数列
,使得数列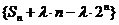 成等差数列。 ……………… 9分
成等差数列。 ……………… 9分
(Ⅲ)∵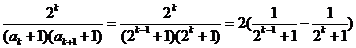 ……………… 10分
……………… 10分
∴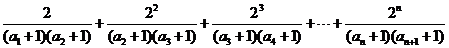
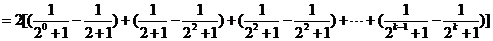
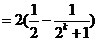 ………………………………………… 12分
………………………………………… 12分
∵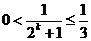 , ∴
, ∴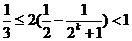 ,
,
∴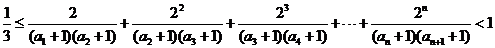 …14分
…14分
20. (本小题满分14分)设数列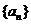 的前
的前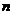 项和为
项和为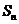 ,且
,且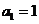 ,
,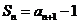 。
。
(Ⅰ) 求数列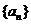 的通项公式;(Ⅱ)是否存在实数
的通项公式;(Ⅱ)是否存在实数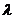 ,使得数列
,使得数列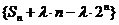 为等差数列?若存在,求出
为等差数列?若存在,求出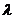 的值;若不存在,则说明理由。
的值;若不存在,则说明理由。
(Ⅲ)求证: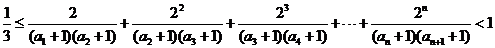 。
。
19. 解析:(I)由题意得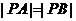 ,
,
∴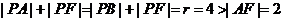
∴P点轨迹是以A、F为焦点的椭圆.………………… 3分
设椭圆方程为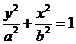
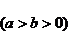 ,
,
则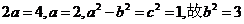 ,
,
∴点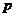 的轨迹方程为
的轨迹方程为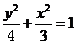 …………………………4分
…………………………4分
曲线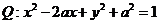 化为
化为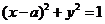 ,
,
则曲线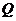 是圆心在
是圆心在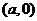 ,半径为1的圆。
,半径为1的圆。
而轨迹E: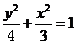 为焦点在Y轴上的椭圆,短轴上的顶点为
为焦点在Y轴上的椭圆,短轴上的顶点为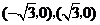 ………6分
………6分
结合它们的图像知:若曲线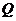 被轨迹E包围着,则
被轨迹E包围着,则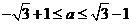
∴ 的最小值为
的最小值为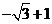 …………………8分
…………………8分
(II))设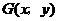 ,由
,由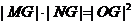 得:
得:
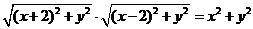 ,
,
化简得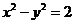 ,即
,即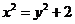 …………………………10分
…………………………10分
而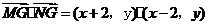
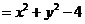
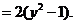
∵点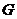 在圆
在圆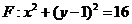 内,∴
内,∴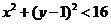
∴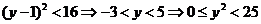 , ………………………12分
, ………………………12分
∴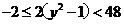 ,∴
,∴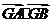 的取值范围为
的取值范围为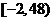 .……………14分
.……………14分
19. (本小题满分14分)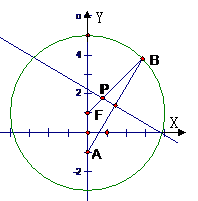 已知定点A(0,-1),点B在圆
已知定点A(0,-1),点B在圆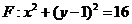 上运动,
上运动,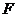 为圆心,线段AB的垂直平分线交BF于P.
为圆心,线段AB的垂直平分线交BF于P.
(I)求动点P的轨迹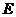 的方程;若曲线
的方程;若曲线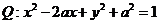 被轨迹
被轨迹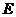 包围着,求实数
包围着,求实数 的最小值。
的最小值。
(II)已知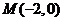 、
、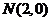 ,动点
,动点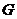 在圆
在圆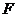 内,且满足
内,且满足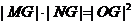 ,求
,求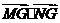 的取值范围.
的取值范围.
21. 解:(Ⅰ)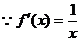 ,
,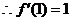 .∴直线
.∴直线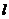 的斜率为
的斜率为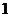 ,且与函数
,且与函数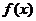 的图象的切点坐标为
的图象的切点坐标为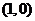 .
∴直线
.
∴直线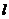 的方程为
的方程为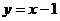 . 又∵直线
. 又∵直线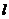 与函数
与函数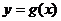 的图象相切,
的图象相切,
∴方程组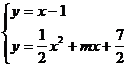 有一解.
由上述方程消去
有一解.
由上述方程消去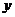 ,并整理得
,并整理得
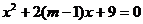 ①
①
依题意,方程①有两个相等的实数根,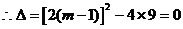
解之,得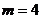 或
或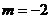
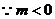
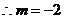 .
.
(Ⅱ)由(Ⅰ)可知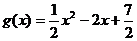 ,
,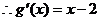
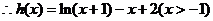 .
. 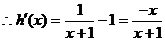 .
.
∴当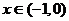 时,
时,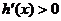 ,当
,当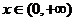 时,
时,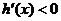 .
.
∴当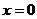 时,
时,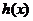 取最大值,其最大值为2.
取最大值,其最大值为2.
(Ⅲ) 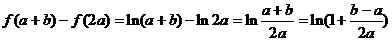 .
.
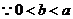 ,
, 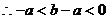 ,
, 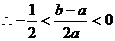 .
.
由(Ⅱ)知当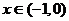 时,
时,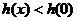 ∴当
∴当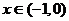 时,
时,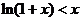 ,
,
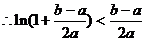 . ∴
. ∴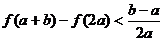
广东二模
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com