
题目列表(包括答案和解析)
20. 设数列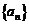 的前
的前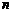 项和为
项和为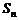 ,已知
,已知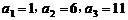 ,且
,且
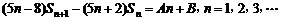 ,
,
其中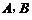 为常数.
为常数.
(Ⅰ)求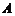 与
与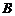 的值;
的值;
(Ⅱ)证明:数列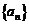 为等差数列;
为等差数列;
(Ⅲ)证明:不等式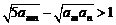 对任何正整数
对任何正整数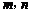 都成立.
都成立.
19. 已知函数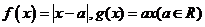 (1)判断函数
(1)判断函数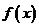 的对称性和奇偶性;(2)当
的对称性和奇偶性;(2)当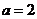 时,求使
时,求使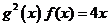 成立的
成立的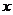 的集合;(3)若
的集合;(3)若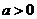 ,记
,记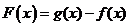 ,且
,且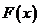 在
在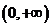 有最大值,求
有最大值,求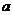 的取值范围.
的取值范围.
18. 已知椭圆C1的方程为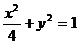 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线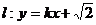 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足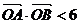 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
17. 甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为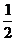 与
与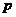 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为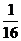 .
.
(Ⅰ)求乙投球的命中率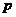 ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为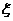 ,求
,求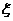 的分布列和数学期望.
的分布列和数学期望.
16.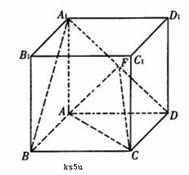 正方体.ABCD-
正方体.ABCD-
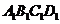 的棱长为l,点F、H分别为为
的棱长为l,点F、H分别为为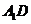 、A1C的中点.
、A1C的中点.
(1)证明: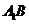 ∥平面AFC;.
∥平面AFC;.
(2)证明B1H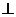 平面AFC.
平面AFC.
15. 已知向量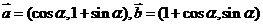 ,(1)若
,(1)若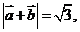 求
求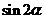 的值;(2)设
的值;(2)设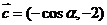 ,求
,求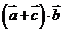 的取值范围.
的取值范围.
14.设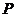 是椭圆
是椭圆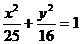 上任意一点,
上任意一点,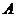 和
和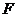 分别是椭圆的左顶点和右焦点,
分别是椭圆的左顶点和右焦点,
则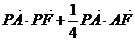 的最小值为
的最小值为
13.已知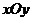 平面内一区域
平面内一区域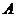 ,命题甲:点
,命题甲:点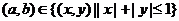 ;命题乙:点
;命题乙:点
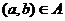 .如果甲是乙的充分条件,那么区域
.如果甲是乙的充分条件,那么区域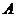 的面积的最小值是
.
的面积的最小值是
.
12.下表是某厂1-4月份用水量(单位:百吨)的一组数据,
月份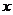 |
1 |
2 |
3 |
4 |
用水量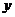 |
4.5 |
4 |
3 |
2.5 |
由其散点图可知,用水量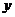 与月份
与月份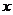 之间有较好的线性相关关系,其线性回归方程
之间有较好的线性相关关系,其线性回归方程
是 .
11.用一些棱长为1cm的小正方体码放成一个几何体,图1为其俯视图,图2为其主视图,则这个几何体的体积最大是 cm3.
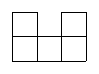
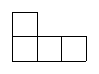
图1(俯视图) 图2(主视图)
第11题图
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com