
题目列表(包括答案和解析)
1. 关于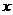 的函数
的函数 有以下命题: ①对任意
有以下命题: ①对任意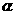 ,
,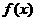 都是非奇非偶函数;
都是非奇非偶函数;
②不存在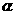 ,使
,使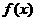 既是奇函数,又是偶函数;③存在
既是奇函数,又是偶函数;③存在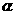 ,使
,使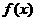 是偶函数;④对任意
是偶函数;④对任意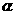 ,
,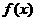 都不是奇函数. 其中一个假命题的序号是 ,因为当
都不是奇函数. 其中一个假命题的序号是 ,因为当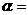 时,该命题的结论不成立.
时,该命题的结论不成立.
6. 在函数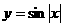 、
、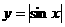 、
、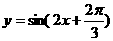 、
、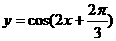 中,
中,
最小正周期为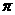 的函数的个数为( )
的函数的个数为( )
A. 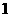 个 B.
个 B. 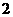 个 C.
个 C. 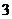 个 D.
个 D. 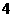 个
个
5. 函数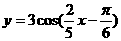 的最小正周期是( )
的最小正周期是( )
A. 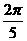 B.
B. 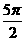 C.
C. 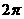 D.
D. 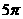
4. 若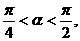 则( )
则( )
A.  B.
B. 
C. 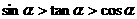 D.
D. 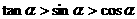
3. 若点 在第一象限,则在
在第一象限,则在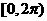 内
内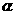 的取值范围是( )
的取值范围是( )
A. 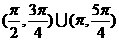 B.
B. 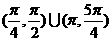
C. 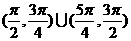 D.
D. 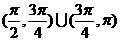
2. 将函数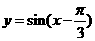 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
再将所得的图象向左平移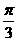 个单位,得到的图象对应的僻析式是( )
个单位,得到的图象对应的僻析式是( )
A. 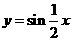 B.
B. 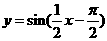
C. 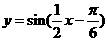 D.
D. 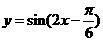
1. 函数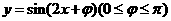 是
是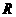 上的偶函数,则
上的偶函数,则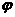 的值是( )
的值是( )
A.  B.
B. 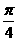 C.
C. 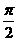 D.
D. 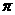
22. (14分)△ABC中,|AB|=|AC|=1,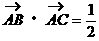 ,P1为AB边上的一点,
,P1为AB边上的一点,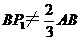 ,从P1向BC作垂线,垂足是Q1;从Q1向CA作垂线,垂足是R1;从R1向AB作垂线,垂足是P2,再由P2开始重复上述作法,依次得Q2,R2,P3;Q3,R3,P4……
,从P1向BC作垂线,垂足是Q1;从Q1向CA作垂线,垂足是R1;从R1向AB作垂线,垂足是P2,再由P2开始重复上述作法,依次得Q2,R2,P3;Q3,R3,P4……
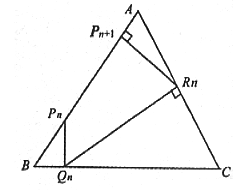
(1)令BPn为xn,寻求BPn与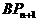 (即
(即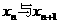 )之间的关系。
)之间的关系。
(2)点列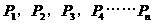 是否一定趋向于某一个定点P0?说明理由;
是否一定趋向于某一个定点P0?说明理由;
(3)若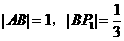 ,则是否存在正整数m,使点P0与Pm之间的距离小于0.001?若存在,求m的最小值。
,则是否存在正整数m,使点P0与Pm之间的距离小于0.001?若存在,求m的最小值。
解:(1)由|AB|=|AC|=1,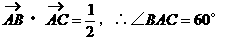
从而△ABC为边长为1的正三角形 2分
则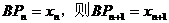 ,于是
,于是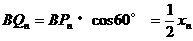
∴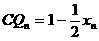 3分
3分
同样 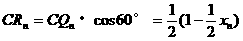
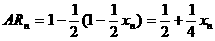 4分
4分
又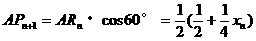
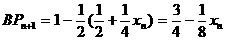
即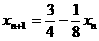 5分
5分
(2)由(1)可得: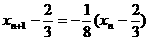
∴ 的等比数列
的等比数列
∴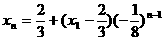 7分
7分
当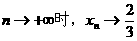
∴点Pn趋向点P0,其中P0在AB上,且BP0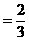 9分
9分
(3)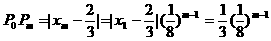 11分
11分
由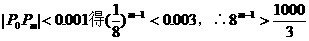
当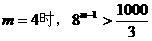
∴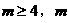 的最小值为4 14分
的最小值为4 14分
21. (12分)已知定点A(0,1),B(0,-1),C(1,0),动点P满足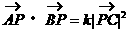
(1)求动点P的轨迹方程,并说明方程表示的曲线。
(2)当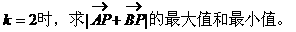
解:(1)设p(x,y)
则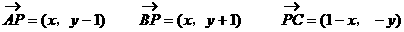
由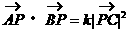 得
得
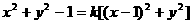 3分
3分
整理得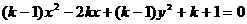 (*) 4分
(*) 4分
当k=1时,*式化为x=1表示直线 5分
当k≠1时,*式化为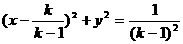
表示心 为半径的圆 6分
为半径的圆 6分
(2)当k=2时,*式化为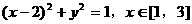
此时,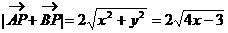
∴其最小值为2,最大值为6 12分
3.德州模拟
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com