
题目列表(包括答案和解析)
2. 已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( ).
A.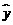 =1.23x+4 B.
=1.23x+4 B. 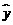 =1.23x+5 C.
=1.23x+5 C. 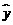 =1.23x+0.08 D.
=1.23x+0.08 D. 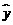 =0.08x+1.23
=0.08x+1.23
|
分组 |
频数 |
频率 |
|
50.5~60.5 |
4 |
0.08 |
|
60.5~70.5 |
|
0.16 |
|
70.5~80.5 |
10 |
|
|
80.5~90.5 |
16 |
0.32 |
|
90.5~100.5 |
|
|
|
合计 |
50 |
|
1. 在40根纤维中,有12根的长度超过30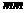 ,从中任取一根,取到长度超过30
,从中任取一根,取到长度超过30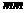 的纤维的概率是( ) A.
的纤维的概率是( ) A.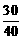 B.
B.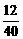 C.
C.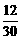 D.以上都不对
D.以上都不对
2. 解: 用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,
且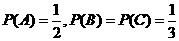 .-------------------------------------------2分
.-------------------------------------------2分
(1)至少有1人面试合格的概率是
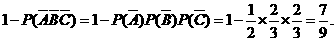 ----------------------4分
----------------------4分
(2)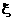 的可能取值为0,1,2,3.------------------------ ---------5分
的可能取值为0,1,2,3.------------------------ ---------5分
∵ 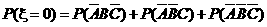
=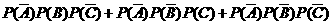
=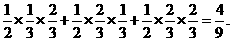 ---------------------------6分
---------------------------6分
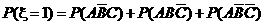
=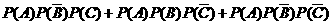
=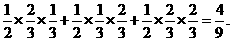 ---------------------7分
---------------------7分
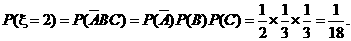 -----------------8分
-----------------8分
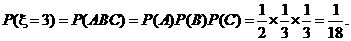 ---------------9分
---------------9分
∴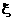 的分布列是
的分布列是
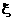 |
0 |
1 |
2 |
3 |
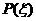 |
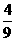 |
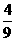 |
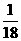 |
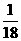 |
--------10分
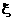 的期望
的期望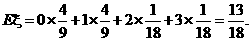 --------------------------12分
--------------------------12分
1.[解题思路]:
(1)由两点分布,分布列易写出,而要求方差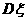 的最大值需求得
的最大值需求得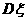 的表达式,转化为二次函数的最值问题;
的表达式,转化为二次函数的最值问题;
(2)得到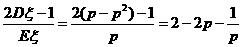 后自然会联想均值不等式求最值。
后自然会联想均值不等式求最值。
解析:(1)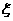 的分布列如表:所以
的分布列如表:所以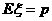 ,
,
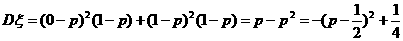
所以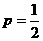 时,
时,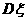 有最大值
有最大值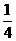 。
。
(2)由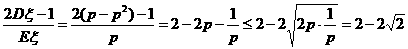 ,当且仅当
,当且仅当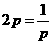 即
即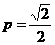 时取等号,所以
时取等号,所以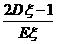 的最大值是
的最大值是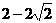 。
。
[名师指引]在超几何分布中,只要知道N,M和n,就可以根据公式求出X取不同m值时的概率P(X=m).
4.解:因为随机变量的概率非负且随机变量取遍所有可能值时相应的概率之和等于1,所以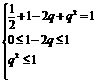 解得
解得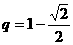 。
。
三解答题:
1.答案: 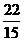 ; 2.答案:
; 2.答案: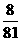
3. 答案: 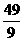 解析:投两个骰子共有36种可能,即
解析:投两个骰子共有36种可能,即
 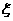 1 1 2 2 |
1 |
2 |
2 |
3 |
3 |
3 |
|
1 2 2 3 3 3 |
1 2 2 3 3 3 |
2 4 4 6 6 6 |
2 4 4 6 6 6 |
3 6 6 9 9 9 |
3 6 6 9 9 9 |
3 6 6 9 9 9 |
∴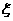 的分布列为
的分布列为
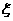 |
1 |
2 |
3 |
4 |
6 |
9 |
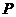 |
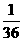 |
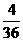 |
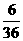 |
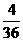 |
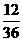 |
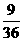 |
∴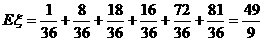
4. 答案:B 解析:这里的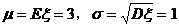 ;由换算关系式
;由换算关系式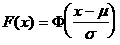 ,有
,有
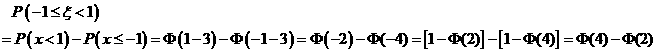 5.答案:C 6.答案:C
5.答案:C 6.答案:C
二填空题:
3.答案:由已知得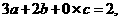 即
即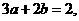
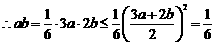 ,故选D.
,故选D.
2.答案:D解析:设二级品有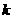 个,∴ 一级品有
个,∴ 一级品有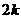 个,三级品有
个,三级品有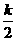 个,总数为
个,总数为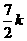 个。
个。
∴ 分布列为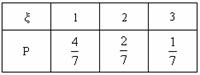
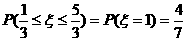
1. 答案:B;[解题思路]: 由离散型随机变量分布列的性质可得
答案:B;[解题思路]: 由离散型随机变量分布列的性质可得
解析:由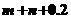
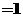 ,又
,又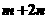
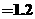 ,可得
,可得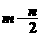
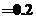
[名师指引]离散型随机变量的分布列都具有下面两个性质:
⑴Pi≥0,i=1,2,…;
⑵P1+P2+…=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com