
题目列表(包括答案和解析)
1.设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B= .
3.[必做题](本题满分10分)
如图所示的几何体是由以等边三角形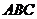 为底面的棱柱被平面
为底面的棱柱被平面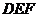 所截而得,已知
所截而得,已知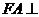 平面
平面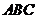 ,
,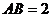 ,
,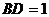 ,
,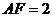 ,
,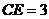 ,
, 为
为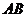 的中点.
的中点.
(Ⅰ)求证: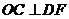 ;
;
(Ⅱ)求平面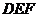 与平面
与平面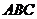 相交所成锐角二面角的余弦值;
相交所成锐角二面角的余弦值;
(Ⅲ)在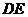 上是否存在一点
上是否存在一点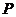 ,使
,使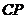
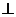 平面
平面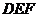 ?如果存在,求出
?如果存在,求出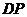 的长;若不存在,说明理由.(选自福州三中第三次月考理)
的长;若不存在,说明理由.(选自福州三中第三次月考理)

提示:如图,以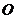 为原点,
为原点,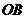 ,
,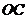 ,
,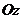 分别为
分别为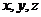 轴建立空间直角坐标系,
轴建立空间直角坐标系,
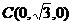 ,
,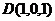 ,
,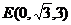 ,
,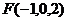 . ……2分
(Ⅰ)
. ……2分
(Ⅰ)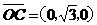 ,
,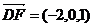 ,
所以
,
所以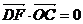 ,即
,即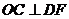 . ……2分
(Ⅱ)平面
. ……2分
(Ⅱ)平面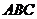 的法向量为
的法向量为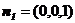 .
设平面
.
设平面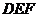 的法向量为
的法向量为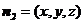 ,
,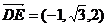 .
由
.
由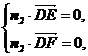 得
得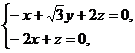 所以
所以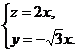 取
取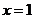 ,得
,得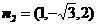 .
所以
.
所以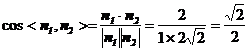 ,所以平面
,所以平面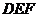 与平面
与平面 相交所成锐角二面角的余弦值为
相交所成锐角二面角的余弦值为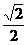 . ……6分
(Ⅲ)假设在
. ……6分
(Ⅲ)假设在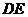 存在一点
存在一点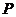 , 设
, 设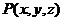 ,
因为
,
因为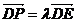 ,故
,故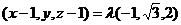 ,
所以
,
所以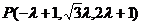 ,所以
,所以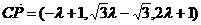 .
因为
.
因为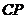
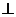 平面
平面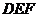 ,所以
,所以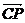 与平面
与平面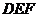 的法向量
的法向量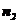 共线,
所以
共线,
所以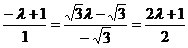 ,解得
,解得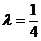 ,
所以
,
所以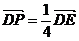 ,即
,即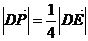 ,所以
,所以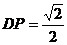 . ……10分
. ……10分
点评:该题考查空间向量的坐标表示、空间向量的数量积、空间向量的共线与垂直、直线的方向向量与平面的法向量;是中档题。
2.[必做题](本题满分10分)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(I)有三人参加抽奖,要使至少一人获奖的概率不低于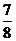 ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张?
(Ⅱ)现有甲乙丙丁四人依次抽奖,用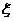 表示获奖的人数,求
表示获奖的人数,求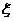 的分布列及
的分布列及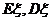 的值.(北京市宣武区理改编)
的值.(北京市宣武区理改编)
提示:(I)记至少一人获奖事件为A,则都不获奖的事件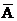 ,设“海宝”卡n张,则任一人获奖的概率
,设“海宝”卡n张,则任一人获奖的概率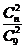 ,所以,
,所以, 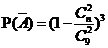 ,由题意:
,由题意: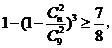 所以,
所以,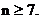
至少7张“海宝”卡………………………………………………4分
(Ⅱ)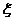 -
-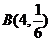 的分布列为
的分布列为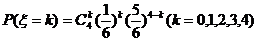 ;
;
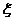 |
0 |
1 |
2 |
3 |
4 |
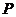 |
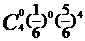 |
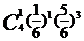 |
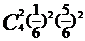 |
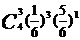 |
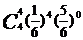 |
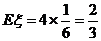 ,
,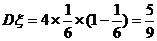 .…………………………………………10分
.…………………………………………10分
点评:该题考查乘法原理、排列组合、二项式定理、n次独立重复试验的模型及二项分布,是中档题。
1.已知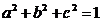 ,若
,若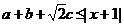 对任意实数a,b,c恒成立,求实数x的取值范围. (选自福建上杭一中12月月考理)
对任意实数a,b,c恒成立,求实数x的取值范围. (选自福建上杭一中12月月考理)
提示: 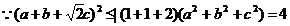
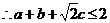 …………………………………………5分
…………………………………………5分
又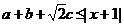 对任意实数a,b,c恒成立,
对任意实数a,b,c恒成立,
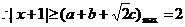
解得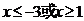 ………………………………………10分
………………………………………10分
点评:该题考查柯西不等式、绝对值不等式求解;是容易题。
3、设关于x的方程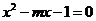 有两个实根
有两个实根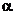 、
、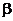 ,且
,且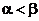 .定义函数
.定义函数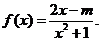
(1)求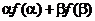 的值;
的值;
(2)判断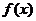 在区间
在区间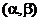 上的单调性,并加以证明;
上的单调性,并加以证明;
(3)若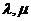 为正实数,证明不等式:
为正实数,证明不等式: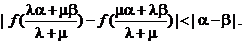
(1)解:∵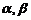 是方程
是方程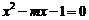 的两个实根
的两个实根
∴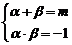
∴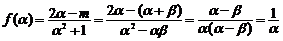
同理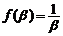
∴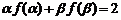 …………3分
…………3分
(2)∵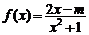
∴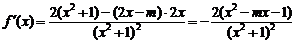 …………4分
…………4分
当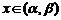 时,
时,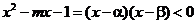
而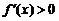
∴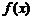 在
在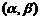 上为增函数
…………7分
上为增函数
…………7分
(3)∵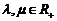 且
且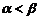
∴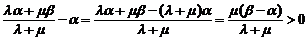
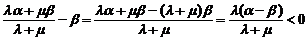
∴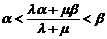 …………9分
…………9分
由(Ⅱ)可知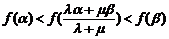
同理可得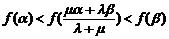 …………9分
…………9分
∴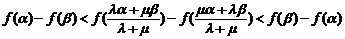
∴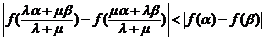 …………11分
…………11分
又由(Ⅰ)知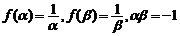
∴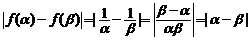
所以 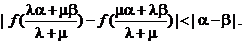 …………12分
…………12分
2、设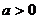 ,函数
,函数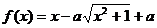 .
.
(1)若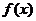 在区间
在区间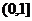 上是增函数,求a的取值范围;
上是增函数,求a的取值范围;
(2)求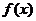 在区间
在区间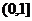 上的最大值.
上的最大值.
(1)解:对函数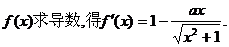 ……………………… 1分
……………………… 1分
要使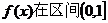 上是增函数,只要
上是增函数,只要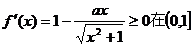 上恒成立,
上恒成立,
即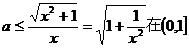 上恒成立 ……………………………………3分
上恒成立 ……………………………………3分
因为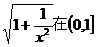 上单调递减,所以
上单调递减,所以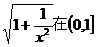 上的最小值是
上的最小值是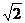 ,
,
注意到a > 0,所以a的取值范围是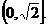 ……………………………………5分
……………………………………5分
(2)解:①当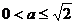 时,由(I)知,
时,由(I)知,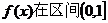 上是增函数,
上是增函数,
此时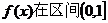 上的最大值是
上的最大值是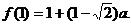 ……………………7分
……………………7分
②当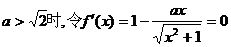 ,
,
解得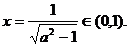 ……………………………………………………8分
……………………………………………………8分
因为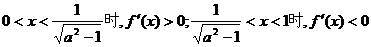 ,
,
所以 上单调递减,
上单调递减,
此时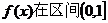 上的最大值是
上的最大值是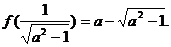 ………… 11分
………… 11分
综上,当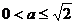 时,
时,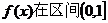 上的最大值是
上的最大值是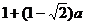 ;
;
当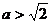 时,
时,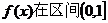 上的最大值是
上的最大值是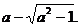 ……………12分
……………12分
1、已知函数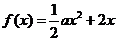 ,
,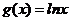 .
.
(1)如果函数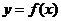 在
在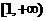 上是单调增函数,求
上是单调增函数,求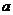 的取值范围;
的取值范围;
(2)是否存在实数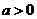 ,使得方程
,使得方程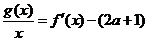 在区间
在区间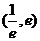 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出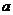 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅰ)解:当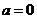 时,
时,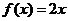 在
在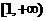 上是单调增函数,符合题意.………1分
上是单调增函数,符合题意.………1分
当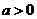 时,
时,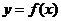 的对称轴方程为
的对称轴方程为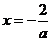 ,
,
由于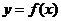 在
在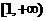 上是单调增函数,
上是单调增函数,
所以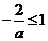 ,解得
,解得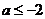 或
或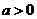 ,
,
所以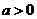 .
……………………2分
.
……………………2分
当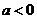 时,不符合题意.
时,不符合题意.
综上,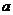 的取值范围是
的取值范围是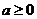 .
……………………3分
.
……………………3分
(Ⅱ)解:把方程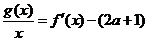 整理为
整理为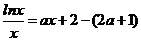 ,
,
即为方程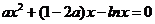 .
……………………4分
.
……………………4分
设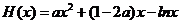
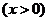 ,
,
原方程在区间(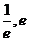 )内有且只有两个不相等的实数根, 即为函数
)内有且只有两个不相等的实数根, 即为函数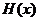 在区间(
在区间(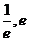 )内有且只有两个零点.
……………………5分
)内有且只有两个零点.
……………………5分
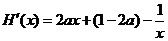
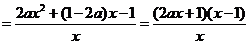 …………………6分
…………………6分
令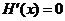 ,因为
,因为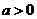 ,解得
,解得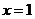 或
或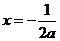 (舍) …………………7分
(舍) …………………7分
当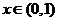 时,
时, 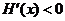 ,
, 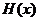 是减函数;
是减函数;
当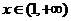 时,
时, 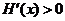 ,
,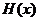 是增函数.
…………………8分
是增函数.
…………………8分
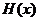 在(
在(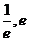 )内有且只有两个不相等的零点, 只需
)内有且只有两个不相等的零点, 只需
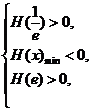 …………………11分
…………………11分
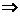
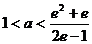 …………………12分
…………………12分
3.已知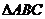 中,角
中,角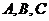 的对边分别是
的对边分别是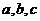 ,且满足
,且满足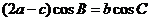 .
.
(1)求角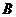 的大小;
的大小;
(2)设 ,
,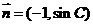 ,求
,求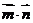 的最小值.
的最小值.
[解析](1)由于弦定理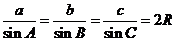 ,
,
有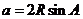 ,
,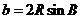 ,
,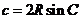
代入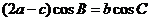 .得
.得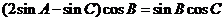 ,
,
即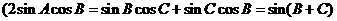 ,
,
∵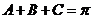 ,∴
,∴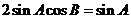 ,
,
∵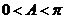 ,∴
,∴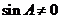 ,∴
,∴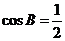 ,
,
∵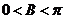 ,∴
,∴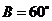 .
.
(2)∵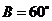 ,∴
,∴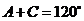 ,
,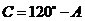 ,
,
∴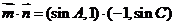
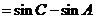
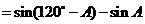
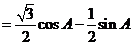
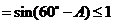 .
.
上式当且仅当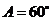 时,取等号,此时
时,取等号,此时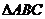 是等边三角形.
是等边三角形.
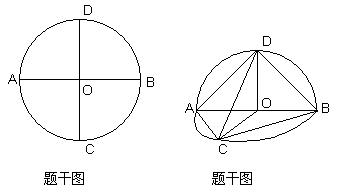
2. 半径为
半径为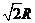 ,
,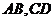 是互相垂直的直径,沿
是互相垂直的直径,沿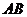 将圆面折成大小为
将圆面折成大小为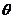 的二面角.
的二面角.
(1)当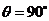 时,求四面体
时,求四面体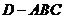 的表面积;
的表面积;
(2)当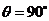 时,求异面直线
时,求异面直线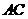 与
与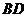 所成的角;
所成的角;
(3)当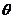 为何值时,四面体
为何值时,四面体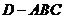 的体积
的体积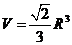 ?
?
[解析](1)由已知,易得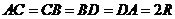 ,
,
∵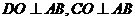
∴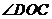 为二面角的平面角
为二面角的平面角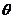 ,在
,在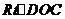 中,得
中,得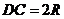
于是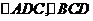 是全等的正三角形,边长为
是全等的正三角形,边长为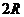 ,而
,而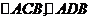 为全等的等腰直角三角形.
为全等的等腰直角三角形.
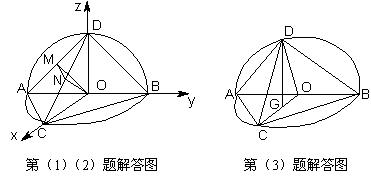
∴四面体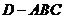 的表面积
的表面积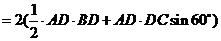
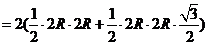
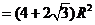 .
.
(2)(方法一)设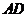 中点为
中点为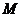 ,
,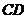 中点为
中点为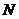 ,连
,连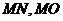 ,则
,则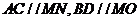 ,
,
则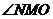 为异面直线
为异面直线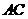 与
与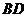 所成的角,连
所成的角,连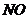 ,由(1)可得
,由(1)可得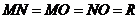 ,
,
所以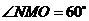 .
.
(方法二)∵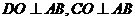 ,
,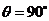
∴分别以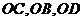 为
为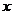 轴、
轴、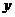 轴、
轴、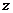 轴建立空间直角坐标系,则有
轴建立空间直角坐标系,则有
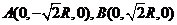 ,
,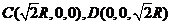
∴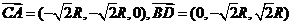
设异面直线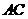 与
与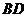 所成的角所成的角为
所成的角所成的角为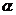 ,
,
则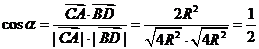
所以异面直线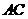 与
与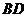 所成的角为
所成的角为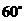 .
.
(3)如图,作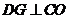 于
于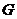 ,
,
∵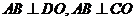 ,∴
,∴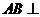 平面
平面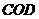 ,从而
,从而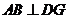
∴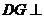 平面
平面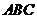 ,∴
,∴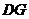 为四面体
为四面体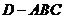 的高,
的高,
在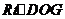 中,
中,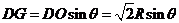 ,
,
∴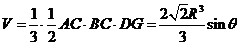 ,
,
当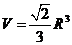 时,解得
时,解得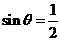 ,所以
,所以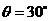 或
或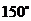 .
.
1. 在海岛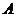 上有一座海拔
上有一座海拔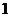 千米的山,山顶设有一个观察站
千米的山,山顶设有一个观察站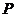 ,上午
,上午 时,测得一轮船在岛北偏东
时,测得一轮船在岛北偏东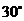 、俯角为
、俯角为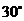 的
的 处,到
处,到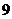 时
时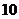 分又测得该船在岛北西
分又测得该船在岛北西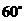 、俯角为
、俯角为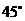 的
的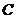 处.
处.
(1)求船的航行速度是每小时多少千米;
(2)在 点处,该船改为向正南方向航行,而不改变速度,
点处,该船改为向正南方向航行,而不改变速度,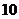 分钟后到达什么位置(以
分钟后到达什么位置(以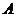 点为参照点)?(参考数据:
点为参照点)?(参考数据: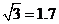 )
)
[解析](1)在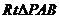 中,
中,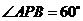 ,
,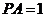 ,∴
,∴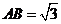 (千米)
(千米)
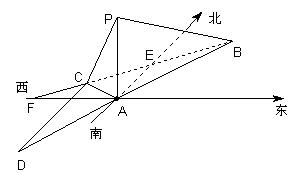
在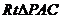 中,
中,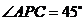 ,
,
∴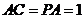 (千米)
(千米)
在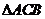 中,
中,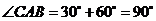
∴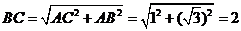
∴船的航行速度是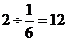 (千米/小时).
(千米/小时).
(2)设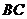 交南北轴于点
交南北轴于点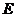 ,延长
,延长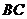 交东西轴于点
交东西轴于点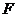 ,则
,则
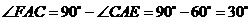 ,
,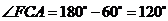 ,
,
设 分钟后该船到达点
分钟后该船到达点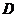 ,因为该船向正南航行,所以
,因为该船向正南航行,所以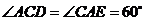 ,
,
 分钟所走的航程是
分钟所走的航程是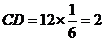 (千米),
(千米),
在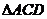 中,由余弦定理得:
中,由余弦定理得: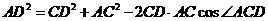
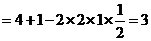 ,∴
,∴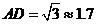 (千米)
(千米)
∴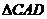 是直角三角形,
是直角三角形,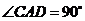 ,而
,而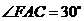 ,
,
∴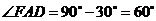 .
.
∴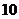 分钟后该船距离在点
分钟后该船距离在点 西偏南
西偏南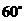 ,距离
,距离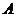 点
点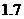 千米处.
千米处.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com