11．已知椭圆C：+＝1(a＞b＞0)，直线l为圆O：x²+y²＝b²的一条切线，且经过椭圆的右焦点，记椭圆离心率为e．

(1)若直线l的倾斜角为，求e的值；

(2)是否存在这样的e，使得原点O关于直线l的对称点恰好在椭圆C上？

若存在，请求出e的值；若不存在，请说明理由．

10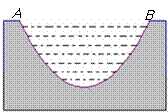．一个截面为抛物线形的旧河道，河口宽AB＝4米，河深2米，现要将其截面改造为等腰梯形，要求河道深度不变，而且施工时只能挖土，不准向河道填土，

试求当截面梯形的下底长为多少米时，才能使挖出的土最少？

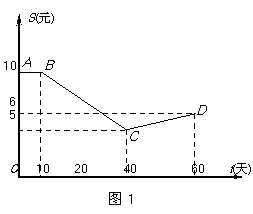
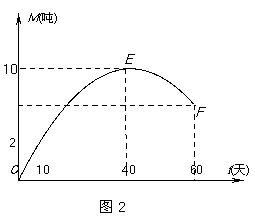
9．时值5月，荔枝上市．某市水果市场由历年的市场行情得知，从5月10日起的60天内，荔枝的售价S(t)(单位：元／kg)与上市时间t(单位：天)的关系大致可用如图1所示的折线ABCD表示，每天的销售量M(t)(单位：吨)与上市时间t(单位：天)的关系大致可用如图2所示的抛物线段OEF表示，其中O为坐标原点，E是抛物线的顶点．

(1)请分别写出S(t)，M(t)关于t的函数关系式；

(2)在这60天内，该水果市场哪天的销售额最大？

8．某观测站C在A城的南偏西20^o的方向，由A城出发有一条公路，公路的走向是南偏东40^o，在C处测得距离为31km的公路上B处，有一人正沿着公路向A城走来，他走了20km后到达D处，此时C，D之间相距21km，问此人还要走多少路才能到达A城？

7．某网球中心欲建连成片的网球场数块，用128万元购买土地10000平方米，该中心每块球场的建设面积为1000平方米，球场的总建筑面积的每平方米的平均建设费用与球场数有关，当该中心建球场x块时，每平方米的平均建设费用(单位：元)可近似地用f(x)＝800(1+lnx)来刻画．为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和)，该网球中心应建几个球场?

6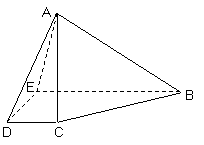．如图，在四棱锥A－BCDE中，底面BCDE是直角梯形，∠BED＝90°，BE∥CD，AB＝6，BC＝5，＝，侧面ABE^底面BCDE．且ÐBAE＝90°．

(1)求证：平面ADE^平面ABE；

(2)过点D作平面a∥平面ABC，分别与BE，AE

交于点F，G，求△DFG的面积．

5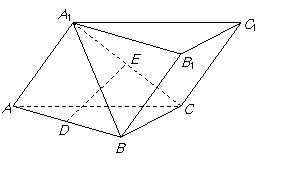．如图，在三棱柱ABC－A₁B₁C₁中，AB＝AC＝2AA₁，ÐBAA₁＝ÐCAA₁＝60°，

D，E分别为AB，A₁C中点．

(1)求证：DE∥平面BB₁C₁C；

(2)求证：BB₁^平面A₁BC．

4．计算：2sin20°+cos10°+tan20°×sin10°．

3．已知函数f(x)＝sin⁴wx+cos⁴wx的相邻对称轴之间的距离为．

(1)求正数w的值；(2)求函数g(x)＝2f(x)+sin²(x+)的最大值及取到最大值时x的值．

2．已知a＝(cosa，sina)，b＝(cosb，sinb)，c＝(1，7sina)，且0＜b＜a＜．

若a×b＝，a∥c．(1)求tanb的值；(2)求cos(2a－b)的值．