
题目列表(包括答案和解析)
20.已知函数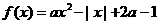 (
(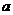 为实常数).
为实常数).
(1)若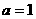 ,作函数
,作函数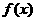 的图像;
的图像;
(2)设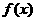 在区间
在区间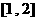 上的最小值为
上的最小值为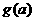 ,求
,求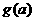 的表达式;
的表达式;
(3)设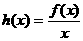 ,若函数
,若函数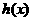 在区间
在区间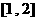 上是增函数,求实数
上是增函数,求实数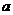 的取值范围.
的取值范围.
解:(1)当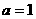 时,
时,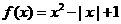
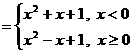 .作图(如右所示)
.作图(如右所示)
(2)当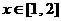 时,
时,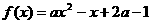 .
.
若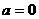 ,则
,则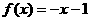 在区间
在区间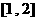 上是减函数,
上是减函数,
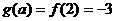 .若
.若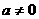 ,则
,则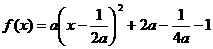 ,
,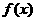 图像的对称轴是直线
图像的对称轴是直线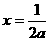 .
.
当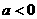 时,
时,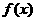 在区间
在区间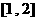 上是减函数,
上是减函数,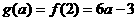 .…
.…
当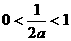 ,即
,即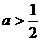 时,
时,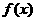 在区间
在区间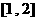 上是增函数,
上是增函数,
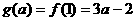 .当
.当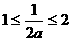 ,即
,即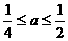 时,
时,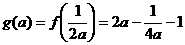 ,…
,…
当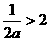 ,即
,即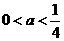 时,
时,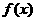 在区间
在区间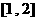 上是减函数,
上是减函数,
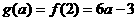 .综上可得
.综上可得
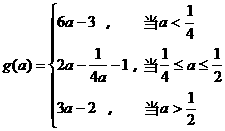 .
.
(3)当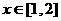 时,
时,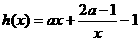 ,在区间
,在区间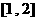 上任取
上任取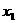 ,
,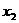 ,且
,且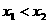 ,
,
则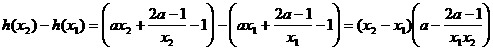
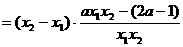 .…
.…
因为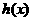 在区间
在区间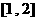 上是增函数,所以
上是增函数,所以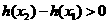 ,
,
因为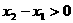 ,
,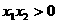 ,所以
,所以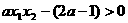 ,即
,即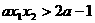 ,
,
当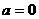 时,上面的不等式变为
时,上面的不等式变为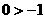 ,即
,即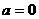 时结论成立.
时结论成立.
当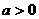 时,
时,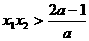 ,由
,由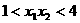 得,
得,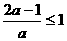 ,解得
,解得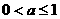 ,
,
当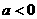 时,
时,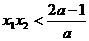 ,由
,由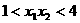 得,
得,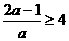 ,解得
,解得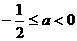 ,
,
所以,实数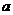 的取值范围为
的取值范围为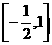 .
.
19.已知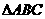 三个顶点分别是A(3,0)、B(0,3)、C
三个顶点分别是A(3,0)、B(0,3)、C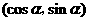 ,其中
,其中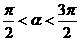 .
.
(1)若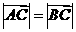 ,求角
,求角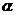 的值;(2)若
的值;(2)若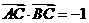 ,求
,求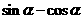 的值.
的值.
解:(1)∵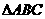 三个顶点分别是A(3,0)、B(0,3)、C
三个顶点分别是A(3,0)、B(0,3)、C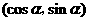 ,
∴
,
∴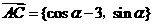 ,
,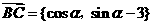
由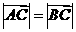 得,
得,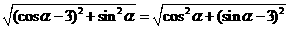
即 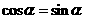 ∵
∵ 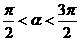 , ∴
, ∴ 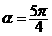 .
.
(2)由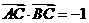 得,
得,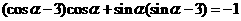
即 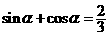 ,
, 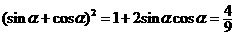 ,
,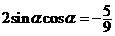
又 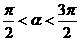 , ∴
, ∴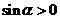 ,
,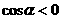
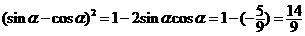 ∴
∴ 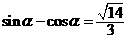 .
.
18.如图,在四棱锥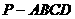 中,底面
中,底面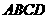 是边长为
是边长为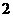 的菱形,
的菱形,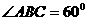 ,
, 平面
平面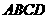 ,
,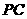 与平面
与平面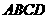 所成角的大小为
所成角的大小为 ,
,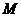 为
为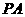 的中点.
的中点.
(1)求四棱锥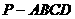 的体积;(2)求异面直线
的体积;(2)求异面直线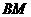 与
与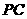 所成角的大小
所成角的大小
解:(1)连结 ,因为
,因为 平面
平面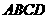 ,
,
所以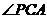 为
为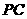 与平面
与平面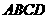 所成的角
所成的角
由已知,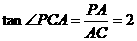 ,而
,而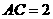 ,
,
所以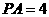 .底面积
.底面积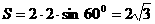 ,
,
所以,四棱锥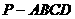 的体积
的体积
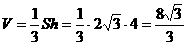 .
.
(2)连结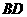 ,交
,交 于点
于点 ,连结
,连结 ,
,
因为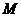 、
、 分别为
分别为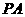 、
、 的中点,所以
的中点,所以 ∥
∥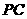 ,
,
所以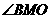 (或其补角)为异面直线
(或其补角)为异面直线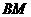 与
与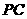 所成的角.)
所成的角.)
在△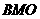 中,
中,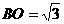 ,
,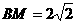 ,
,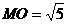 ,
,
(以下由余弦定理,或说明△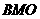 是直角三角形求得)
是直角三角形求得)
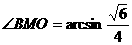 或
或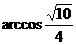 或
或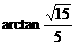 .)
.)
17.若集合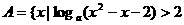 ,
,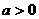 且
且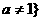
(1)若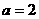 ,求集合
,求集合 ;
;
(2)若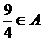 ,求
,求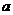 的取值范围.
的取值范围.
(1)若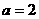 ,
,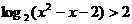 ,则
,则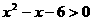 ,
,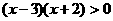 ,
,
得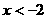 或
或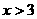 所以
所以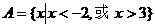
(2)因为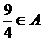 ,所以
,所以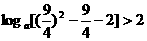
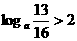 , 因为
, 因为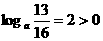
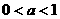 且
且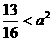 ………………11分
………………11分 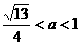
16.若不等式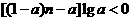 对于任意正整数
对于任意正整数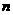 恒成立,则实数
恒成立,则实数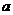 的取值范围是( C )
的取值范围是( C )
A.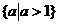 . B.
. B.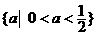 .
.
C.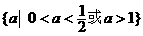 .
D.
.
D.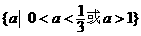 .
.
15.某工厂对一批产品进行了抽样检测.右图是根据
抽样检测后的 产品净重(单位:克)数据绘制的频
率分布直方图,其中产品净重的范围是[96,106],
样本数据分组为[96,98),[98,100),[100,102),
[102,104),[104,106],已知样本中产品净重小于
100克的个数是36,则样本中净重大于或等于98
克并且小于104克的产品的个数是 ( A ).
A.90 B.75 C.60 D.45
14.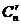 (
(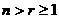 ,
,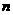 ,
,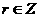 )恒等于………………………………………………( A )
)恒等于………………………………………………( A )
A.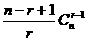 B.
B.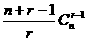 C.
C.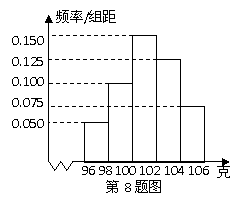
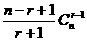 D.
D.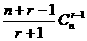
13.已知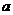 ,
,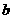 都是实数,则“
都是实数,则“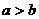 ”是“
”是“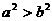 ”的………………………………( D )
”的………………………………( D )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
12.在实数数列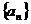 中,已知
中,已知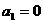 ,
,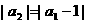 ,
,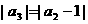 ,…,
,…,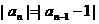 ,则
,则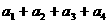 的最大值为
的最大值为 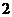 .
.
11.下列有关平面向量分解定理的四个命题中,
所有正确命题的序号是 (2)(3) .
⑤ 一个平面内有且只有一对不平行的向量可
作为表示该平面所有向量的基;
⑥ 一个平面内有无数多对不平行向量可作为
表示该平面内所有向量的基;
⑦ 平面向量的基向量可能互相垂直;
⑧一个平面内任一非零向量都可唯一地表示成
该平面内三个互不平行向量的线性组合.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com